题目内容
(2002•淮安)写出图象经过点(1,0)、(0,1)的三个不同的函数解析式:
y=-x+1,y=
x2-
x+1,y=-x2+1
| 1 |
| 2 |
| 3 |
| 2 |
y=-x+1,y=
x2-
x+1,y=-x2+1
.| 1 |
| 2 |
| 3 |
| 2 |
分析:(1)可设函数为一次函数为y=kx+b,将点(1,0)、(0,1)分别代入解析式,求出k、b的值;
(2)设函数为y=ax2+bx+c,将点(1,0)、(0,1)、(2,0)分别代入解析式,求出a、b、c的值;
(3)设函数为y=ax2+c,将点(1,0)、(0,1)分别代入解析式,求出a、c的值;
从而可得三个不同的解析式.
(2)设函数为y=ax2+bx+c,将点(1,0)、(0,1)、(2,0)分别代入解析式,求出a、b、c的值;
(3)设函数为y=ax2+c,将点(1,0)、(0,1)分别代入解析式,求出a、c的值;
从而可得三个不同的解析式.
解答:解:(1)设函数为一次函数为y=kx+b,
将点(1,0)、(0,1)分别代入解析式得:
,
解得
,
函数解析式为y=-x+1;
(2)设函数为y=ax2+bx+c,
将点(1,0)、(0,1)、(2,0)分别代入解析式得:
,
解得
,
函数解析式为y=
x2-
x+1.
(3)设函数为y=ax2+c,将点(1,0)、(0,1)分别代入解析式得,
,
解得
,
函数解析式为y=-x2+1.
故答案为y=-x+1,y=
x2-
x+1,y=-x2+1.
将点(1,0)、(0,1)分别代入解析式得:
|
解得
|
函数解析式为y=-x+1;
(2)设函数为y=ax2+bx+c,
将点(1,0)、(0,1)、(2,0)分别代入解析式得:
|
解得
|
函数解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(3)设函数为y=ax2+c,将点(1,0)、(0,1)分别代入解析式得,
|
解得
|
函数解析式为y=-x2+1.
故答案为y=-x+1,y=
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了待定系数法求函数解析式,要熟悉各种函数的一般表达式,方可解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
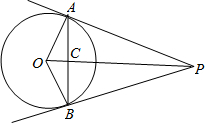 (2002•淮安)如图,PA,PB是⊙O的两条切线,A、B为切点,线段OP交AB于点C,根据题中所给出的条件及图中线段,找出图中线段的乘积关系
(2002•淮安)如图,PA,PB是⊙O的两条切线,A、B为切点,线段OP交AB于点C,根据题中所给出的条件及图中线段,找出图中线段的乘积关系