题目内容
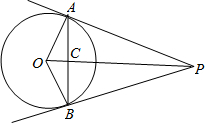（2002•淮安）如图，PA，PB是⊙O的两条切线，A、B为切点，线段OP交AB于点C，根据题中所给出的条件及图中线段，找出图中线段的乘积关系PA2=PC•OP
PA2=PC•OP
，（写出一个乘积等式即可）．分析：根据切线的性质和切线长定理以及等腰三角形的性质可判定△PAO∽△PCA，根据相似的性质得到比例式，进而得到线段的乘积关系．
解答：解：PA2=PC•OP，
理由如下：
∵PA，PB是⊙O的两条切线，A、B为切点，
∴PA=PB，∠APC=∠BPC，
∴PC⊥AB，
∴∠ACP=90°，
∵PA，⊙O的切线，
∴∠OAP=90°，
∵∠APO=∠APO，
∴△PAO∽△PCA，
∴
=
，
∴PA2=PC•OP，
故答案为：PA2=PC•OP．
理由如下：
∵PA，PB是⊙O的两条切线，A、B为切点，
∴PA=PB，∠APC=∠BPC，
∴PC⊥AB，
∴∠ACP=90°，
∵PA，⊙O的切线，
∴∠OAP=90°，
∵∠APO=∠APO，
∴△PAO∽△PCA，
∴
| PA |
| PC |
| PO |
| PA |
∴PA2=PC•OP，
故答案为：PA2=PC•OP．
点评：本题考查了切线的性质和切线长定理以及等腰三角形的性质和相似三角形的判定、判定，本题属于结论开放题目答案不唯一．
练习册系列答案
考前必练系列答案
相关题目
（2002•淮安）如图，在⊙O中，直径MN垂直于弦AB，垂足为C，下面结论中错误是（ ）
（2002•淮安）（1）已知关于x的方程x2-2ax+a2-2a+2=0的两个实数根x1，x2满足x12+x22=2，求a的值．