题目内容
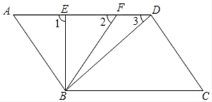
【题目】如图,AB∥CD,AB=CD,点B、E、F、D在同一条直线上,∠BAE=∠DCF.
(1)求证:AE=CF;
(2)连结AF、EC,试猜想四边形AECF是什么四边形,并证明你的结论.
【答案】(1)证明见解析(2)四边形AECF是平行四边形
【解析】
(1)要证AE=CF,可证△ABE≌△CDF.由AB∥CD,可知∠B=∠D,由AB=CD,已知∠BAE=∠DCF,即可证得.
(2)由△ABE≌△CDF得AE=CF,∠AEB=∠CFD,故180°-∠AEB=180°-∠CFD,即∠AEF=∠CFE,AE∥CF,AE=CF,故四边形AECF是平行四边形.
(1)证明:∵AB∥CD,∴∠B=∠D.
在△ABE和△CDF中,
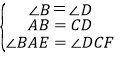 ,
,
∴△ABE≌△CDF,
∴AE=CF.
(2)四边形AECF是平行四边形.
证明:由(1)△ABE≌△CDF得AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,
即∠AEF=∠CFE.
∴AE∥CF.
又∵AE=CF,
∴四边形AECF是平行四边形.
故答案为:(1)证明见解析(2)四边形AECF是平行四边形.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目