题目内容
在等腰△ABC中，AB=AC=13，BC=10，则腰AB上的高为________．
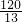
分析：作AD⊥BC于D，CE⊥AB于E．根据等腰三角形的三线合一，得BD=5，根据勾股定理，得AD=12．再根据三角形的面积公式就可求得等腰三角形的腰上的高．
解答：
解：作AD⊥BC于D，CE⊥AB于E．∵AB=AC=13，BC=10，
∴BD=5．
根据勾股定理，得AD=12．
又AB•CE=BC•AD，
则CE=
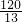=．点评：此题综合运用了等腰三角形的三线合一、勾股定理以及三角形的面积公式．
练习册系列答案
名题金卷系列答案
优加精卷系列答案
相关题目
8、如图所示，在等腰△ABC中，点D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F，图中有几对全等三角形（ ）
（2013•闸北区二模）如图，在等腰△ABC中，底边BC的中点是点D，底角的正切值是
如图，在等腰△ABC中，AB=AC=10cm，直线DE垂直平分AB，分别交AB、AC于D、E两点．若BC=8cm，则△BCE的周长是
如图，在等腰△ABC中，∠ABC=90°，D为底边AC中点，过D点作DE⊥DF，交AB于E，交BC于F．若AE=12，FC=5，