题目内容
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°.
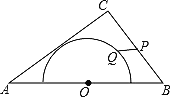
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
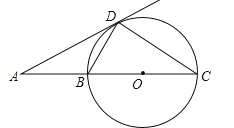
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
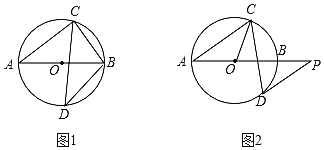
【答案】(1)∠ABC=52°,∠ABD=45°;(2)∠OCD=26°.
【解析】
(1)根据圆周角和圆心角的关系和图形可以求得∠ABC和∠ABD的大小;
(2)根据题意和平行线的性质、切线的性质可以求得∠OCD的大小.
(1)∵AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,∴∠ACB=90°,∴∠ABC=∠ACB﹣∠BAC=90°﹣38°=52°.
∵D为![]() 的中点,∠AOB=180°,∴∠AOD=90°,∴∠ABD=45°;
的中点,∠AOB=180°,∴∠AOD=90°,∴∠ABD=45°;
(2)连接OD.
∵DP切⊙O于点D,∴OD⊥DP,即∠ODP=90°,由DP∥AC,又∠BAC=38°,∴∠P=∠BAC=38°.
∵∠AOD是△ODP的一个外角,∴∠AOD=∠P+∠ODP=128°,∴∠ACD=64°.
∵OC=OA,∠BAC=38°,∴∠OCA=∠BAC=38°,∴∠OCD=∠ACD﹣∠OCA=64°﹣38°=26°.

练习册系列答案
相关题目