题目内容
等腰三角形ABC中,AB=AC,BE、CD分别是∠ABC、∠ACB的角平分线,且BE与CD交于O点,那么你能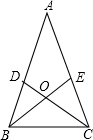 判断△OBC是什么三角形吗?
判断△OBC是什么三角形吗?解:∵△ABC是等腰三角形,AB=AC
∴∠
∵BE、CD分别是∠ABC、∠ACB的角平分线
∴∠EBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠
∴△OBC是
分析:根据等边对等角,等角对等边和角平分线的定义填空即可.
解答:解:ABC,ACB,等边对等角;
ABC,ACB;
EBC,DCB,
等腰,等角对等边.
ABC,ACB;
EBC,DCB,
等腰,等角对等边.
点评:本题考查等腰三角形的性质和判定以及角平分线的定义,主要在于训练同学们的证明书写过程.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
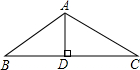 如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD=
如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD= 如图,等腰三角形ABC中,AB=AC,AD是底边BC上的中线,若AB=10,BC=12,则中线AD的长度为( )
如图,等腰三角形ABC中,AB=AC,AD是底边BC上的中线,若AB=10,BC=12,则中线AD的长度为( )