题目内容
问题：如图1，在正方形ABCD内有一点P，PA=
，PB=
，PC=1，求∠BPC的度数．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′．
请你参考小明同学的思路，解决下列问题：
(1) 图2中∠BPC的度数为 ；
(2) 如图3，若在正六边形ABCDEF内有一点P，且PA=
，PB=4，PC=2，则∠BPC的度数为 ，正六边形ABCDEF的边长为 ．
(1)135° (2) 120° 
解析试题分析:解：（1）135°；………………………………………………………………………… 2分
（2）120°；………………………………………………………………………… 3分 ． ……………………………………………………………………… 5分
考点：本题考察了图形转换的知识。
点评：解答此题的关键，是进行巧妙地旋转变换。让每一点P绕一固定点(固定轴线)旋转一个定角，变成另一点P′，如此产生的变换称为平面上(空间中)的旋转变换，它是欧氏几何中的一种重要变换，是解答解析几何数学题的一种重要思想。
练习册系列答案
相关题目
甲乙两辆汽车在一条公路上匀速行驶．为了确定汽车的位置，我们用数轴Ox表示这条公路，原点O为零千米路标（如图），
并作如下约定：
①速度v＞0．表示汽车向数轴正方向行驶；
速度v＜0，表示汽车向数轴负方向行驶；
速度v=0，表示汽车静止．
②汽车位置在数轴上的坐标s＞0，表示汽车位于零千米路标的右侧；
汽车位置在数轴上的坐标s＜0，表示汽车位于零千米路标的左侧；
汽车位置在数轴上的坐标s=0，表示汽车恰好位于零千米路标处．
遵照上述约定，将这两辆汽车在公路上匀速行驶的情况，以一次函数图象的形式画在了同一直角坐标系中，如图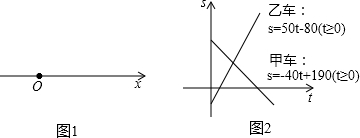
请解答下列问题：
（1）就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格．
（2）甲乙两车能否相遇如能相遇，求相遇时的时刻及在公路上的位置；如不能相遇，请说理由．
并作如下约定：
①速度v＞0．表示汽车向数轴正方向行驶；
速度v＜0，表示汽车向数轴负方向行驶；
速度v=0，表示汽车静止．
②汽车位置在数轴上的坐标s＞0，表示汽车位于零千米路标的右侧；
汽车位置在数轴上的坐标s＜0，表示汽车位于零千米路标的左侧；
汽车位置在数轴上的坐标s=0，表示汽车恰好位于零千米路标处．
遵照上述约定，将这两辆汽车在公路上匀速行驶的情况，以一次函数图象的形式画在了同一直角坐标系中，如图
请解答下列问题：
（1）就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格．
| 行驶方向 | 速度的大小（km/h） | 出发前的位置 | |
| 甲车 | |||
| 乙车 |
