Question

如图，一次函数y₁＝k₁x＋b₁与y₂＝k₂x＋b₂的图象相交于A(3，2)，则不等式(k₂－k₁)x＋b₂－b₁＞0的解集为__________.

 

Answer 1

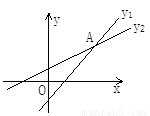
【答案】

x＜3

【解析】

试题分析：由(k₂－k₁)x＋b₂－b₁＞0可得k₂ x－k₁x＋b₂－b₁＞0，即k₂ x＋b₂＞k₁x+b₁，找到函数y₁＝k₁x＋b₁的图像在函数y₂＝k₂x＋b₂的图象下方的部分即可.

∵(k₂－k₁)x＋b₂－b₁＞0

∴k₂ x－k₁x＋b₂－b₁＞0

∴k₂ x＋b₂＞k₁x+b₁

∵一次函数y₁＝k₁x＋b₁与y₂＝k₂x＋b₂的图象相交于A(3，2)

∴不等式(k₂－k₁)x＋b₂－b₁＞0的解集为x＜3.

考点：本题考查的是一元一次不等式与一次函数

点评：解答本题的关键是理解函数y₁＝k₁x＋b₁的图像在函数y₂＝k₂x＋b₂的图象下方的部分即为不等式(k₂－k₁)x＋b₂－b₁＞0的解集.