题目内容
如图,已知矩形A′BOC的边长A′B=2,OB=1,数轴上点A表示的数为x,则x2-13的立方根是
- A.
 -13
-13 - B.-
 -13
-13 - C.2
- D.-2
D
分析:先将原式x2-13变形为x2-4-9,整体求出x2-4的值,然后根据立方根的定义来解答.
解答:根据勾股定理x2-22=12,即x2-22=1,
∴x2-13=x2-4-9=1-9=-8,
则x2-13的立方根是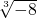 =-2.
=-2.
故选D.
点评:本题综合性较强,不仅要结合图形,还需要熟悉勾股定理和立方根的定义.
分析:先将原式x2-13变形为x2-4-9,整体求出x2-4的值,然后根据立方根的定义来解答.
解答:根据勾股定理x2-22=12,即x2-22=1,
∴x2-13=x2-4-9=1-9=-8,
则x2-13的立方根是
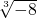 =-2.
=-2.故选D.
点评:本题综合性较强,不仅要结合图形,还需要熟悉勾股定理和立方根的定义.

练习册系列答案
相关题目
如图,已知矩形A′BOC的边长A′B=2,OB=1,数轴上点A表示的数为x,则x2-13的立方根是( )

A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
 9、如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形(含三角形),若这两个多边形的内角和分别为M和N,则M+N不可能是( )
9、如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形(含三角形),若这两个多边形的内角和分别为M和N,则M+N不可能是( ) 27、如图,已知矩形ABCD中,AC与BD相交于O,DE平分∠ADC交BC于E,∠BDE=15°,则∠COE的度数为
27、如图,已知矩形ABCD中,AC与BD相交于O,DE平分∠ADC交BC于E,∠BDE=15°,则∠COE的度数为 如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点,P异于A、D,Q是BC边上的一动点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点,P异于A、D,Q是BC边上的一动点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F. (2012•南湖区二模)如图,已知矩形ABCD中,过点C作CE∥DB,交AB的延长线与E.求证:△ACE是等腰三角形.
(2012•南湖区二模)如图,已知矩形ABCD中,过点C作CE∥DB,交AB的延长线与E.求证:△ACE是等腰三角形.