题目内容
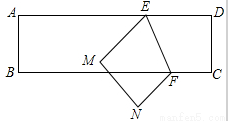
如图,在ΔABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30 DF=2 ,AF=BF,则四边形BCDE的周长为( )

A、4 B、8 C、 4+4
B、8 C、 4+4 D、8+4
D、8+4
D
【解析】
试题分析:因为DE是AC的垂直的平分线,所以D是AC的中点,F是AB的中点,所以DF BC,所以∠C=90°,所以四边形BCDE是矩形,因为∠A=30°,∠C=90°,BC=4,能求出AB的长,根据勾股定理求出AC的长,从而求出DC的长,从而求出周长.
BC,所以∠C=90°,所以四边形BCDE是矩形,因为∠A=30°,∠C=90°,BC=4,能求出AB的长,根据勾股定理求出AC的长,从而求出DC的长,从而求出周长.
∵DE是AC的垂直的平分线,F是AB的中点,
∴DF∥BC,且BC= DF=4,
DF=4,
∴∠C=90°,
∴四边形BCDE是矩形.
∵∠A=30°,∠C=90°,BC=4,
∴AB=8,
∴AC= ∴BE=CD=
∴BE=CD= .
.
∴四边形BCDE的周长为:2×(4+ )=8+
)=8+ .
.
故选D.
考点:1. 矩形的判定与性质;2.线段垂直平分线的性质;3.勾股定理.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目








 的图象如图,则一元二次方程
的图象如图,则一元二次方程 根的情况是( )
根的情况是( )