题目内容
某“研究性学习小组”遇到了以下问题,请参与:已知,△ABC是等边三角形且内接于⊙O,取
 上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.



(1)如图1,图2,图3,M分别为
 的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
 上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______;
上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______;(3)对(2)中提出的猜想,依图4给出证明.
【答案】分析:本题要求的实际是AK、BN与等边三角形ABC边长的关系.可通过证△AKB与△BAN相似来求解.
解答: 解:(1)4,4,4
解:(1)4,4,4
(2)AK•BN=AB2
(3)∵∠ABM+∠BAM=∠AMK=∠C=60°,∠BAM+∠N=60°
∴∠ABM=∠N
∵∠KAB=∠NBA=120°
∴△AKB∽△BAN
∴
∴AK•BN=AB2.
点评:本题主要考查了圆周角定理,相似三角形的判定和性质,等边三角形的性质等知识点.根据圆周角定理得出角相等从而证得三角形相似是解题的关键.
解答:
 解:(1)4,4,4
解:(1)4,4,4(2)AK•BN=AB2
(3)∵∠ABM+∠BAM=∠AMK=∠C=60°,∠BAM+∠N=60°
∴∠ABM=∠N
∵∠KAB=∠NBA=120°
∴△AKB∽△BAN
∴

∴AK•BN=AB2.
点评:本题主要考查了圆周角定理,相似三角形的判定和性质,等边三角形的性质等知识点.根据圆周角定理得出角相等从而证得三角形相似是解题的关键.

练习册系列答案
相关题目


 23、某研究性学习小组,为了了解某校七年级学生一天中做家庭作业所用的大致时间(时间以整数记.单位:分),对本校的初一学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图),请结合统计图中提供的信息,回答下列问题.
23、某研究性学习小组,为了了解某校七年级学生一天中做家庭作业所用的大致时间(时间以整数记.单位:分),对本校的初一学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图),请结合统计图中提供的信息,回答下列问题. 14、某研究性学习小组,为了了解本校八年级学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本年级同学做了抽样调查,并整理绘制成直方图如图所示.
14、某研究性学习小组,为了了解本校八年级学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本年级同学做了抽样调查,并整理绘制成直方图如图所示.
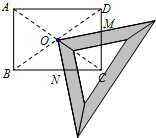 某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于