题目内容
6.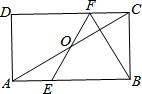 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为6.
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为6.
分析 先证明△AOE≌△COF,RT△BFO≌RT△BFC,再证明△OBC、△BEF是等边三角形即可就问题.
解答 解:如图,连接BO,
∵四边形ABCD是矩形,
∴DC∥AB,∠DCB=90°
∴∠FCO=∠EAO,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠AOE=∠FOC}\\{∠FCO=∠EAO}\\{AE=CF}\end{array}\right.$,
∴△AOE≌△COF,
∴OE=OF,OA=OC,
∵BF=BE,
∴BO⊥EF,∠BOF=90°,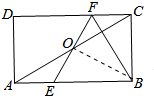
∵∠FEB=2∠CAB=∠CAB+∠AOE,
∴∠EAO=∠EOA,
∴EA=EO=OF=FC=2,
在RT△BFO和RT△BFC中,
$\left\{\begin{array}{l}{BF=BF}\\{FO=FC}\end{array}\right.$,
∴RT△BFO≌RT△BFC,
∴BO=BC,
在RT△ABC中,∵AO=OC,
∴BO=AO=OC=BC,
∴△BOC是等边三角形,
∴∠BCO=60°,∠BAC=30°,
∴∠FEB=2∠CAB=60°,∵BE=BF,
∴△BEF是等边三角形,
∴EB=EF=4,
∴AB=AE+EB=2+4=6.
故答案为6.
点评 本题考查矩形的性质、全等三角形的判定和性质、等边三角形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是正确寻找全等三角形,利用全等三角形的性质就问题,属于中考常考题型.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
11.一个等腰三角形的顶角为110°,则底角是( )
| A. | 10° | B. | 30° | C. | 40° | D. | 35° |
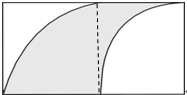 如图,由两个边长为6米的正方形拼成一个长方形.求图中阴影部分的面积.
如图,由两个边长为6米的正方形拼成一个长方形.求图中阴影部分的面积.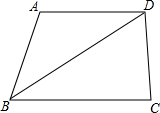 已知:如图,BD平分∠ABC,AD∥BC.求证:AB=AD.
已知:如图,BD平分∠ABC,AD∥BC.求证:AB=AD.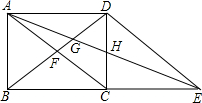 如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.
如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.