题目内容
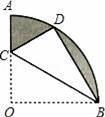
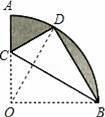
如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,整个阴影部分的面积 .

9π﹣12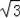
 .
.
【考点】翻折变换(折叠问题);扇形面积的计算.
【分析】首先连接OD,由折叠的性质,可得CD=CO,BD=BO,∠DBC=∠OBC,则可得△OBD是等边三角形,继而求得OC的长,即可求得△OBC与△BCD的面积,又在扇形OAB中,∠AOB=90°,半径OA=6,即可求得扇形OAB的面积,继而求得阴影部分面积.
【解答】解:连接OD.
根据折叠的性质,CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,
即△OBD是等边三角形,
∴∠DBO=60°,
∴∠CBO=
 ∠DBO=30°,
∠DBO=30°,
∵∠AOB=90°,
∴OC=OB•tan∠CBO=6×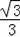
 =2
=2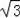
 ,
,
∴S△BDC=S△OBC=
 ×OB×OC=
×OB×OC=
 ×6×2
×6×2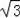
 =6
=6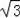
 ,S扇形AOB=
,S扇形AOB=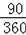
 π×62=9π,
π×62=9π,
∴整个阴影部分的面积为:S扇形AOB﹣S△BDC﹣S△OBC=9π﹣6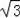
 ﹣6
﹣6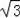
 =9π﹣12
=9π﹣12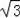
 .
.
故答案为:9π﹣12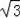
 .
.

【点评】此题考查了折叠的性质、扇形面积公式以及直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
相关题目

 +2的值是在( )
+2的值是在( )