题目内容
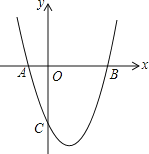
【题目】如图①,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,二次函数的对称轴与
,二次函数的对称轴与![]() 轴的交于点
轴的交于点![]() ,作射线
,作射线![]() .
.
![]() 抛物线
抛物线![]() 的解析式为 ; 点
的解析式为 ; 点![]() 坐标为_ ;
坐标为_ ;
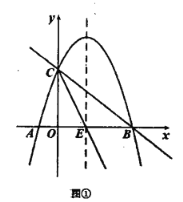
![]() 求证:射线
求证:射线![]() 是
是![]() 的角平分线;
的角平分线;
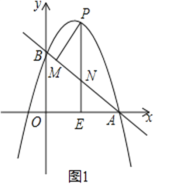
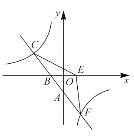
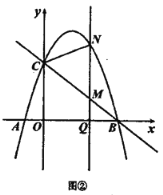
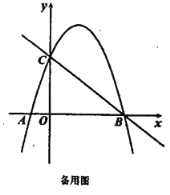
![]() 如图②,点
如图②,点![]() 是
是![]() 的正半轴上一点,过点
的正半轴上一点,过点![]() 作
作![]() 轴的平行线,与直线
轴的平行线,与直线![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,连结
,连结![]() ,将
,将![]() 沿
沿![]() 翻折,
翻折,![]() 的对应点为
的对应点为![]() .在图②中探究;是否存在点
.在图②中探究;是否存在点![]() ,使褥
,使褥![]() 恰好落在
恰好落在![]() 轴的正半轴上?若存在,请求出
轴的正半轴上?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)见解析(3)存在,
(2)见解析(3)存在,![]()
【解析】
(1)根据点![]() ,
,![]() 的坐标,利用待定系数法即可求出二次函数的表达式;把抛物线的表达式化成顶点式得到点
的坐标,利用待定系数法即可求出二次函数的表达式;把抛物线的表达式化成顶点式得到点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,先计算出OC、BC、BE的长度,再利用三角函数计算出EF的长度,证得
,先计算出OC、BC、BE的长度,再利用三角函数计算出EF的长度,证得![]() ,从而证出射线
,从而证出射线![]() 是
是![]() 的角平分线;
的角平分线;
(3)利用二次函数图象上点的坐标特征可求出点![]() 的坐标,由点
的坐标,由点![]() ,
,![]() 的坐标利用待定系数法可求出直线
的坐标利用待定系数法可求出直线![]() 的函数表达式,由点
的函数表达式,由点![]() 的坐标可得出点
的坐标可得出点![]() ,
,![]() 的坐标,进而可得出
的坐标,进而可得出![]() 的长度,结合点
的长度,结合点![]() 的坐标可得出
的坐标可得出![]() 的长度,由菱形的性质可得出
的长度,由菱形的性质可得出![]() ,进而可得出关于
,进而可得出关于![]() 的一元二次方程,解之即可得出
的一元二次方程,解之即可得出![]() 的值(取正值),进而可得出点
的值(取正值),进而可得出点![]() 的坐标;
的坐标;
解:(1)将![]() ,
,![]() 代入
代入![]() ,得:
,得:
![]() ,解得:
,解得: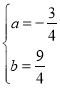 ,
,
![]() 二次函数的表达式为
二次函数的表达式为![]() .
.
![]()
![]()
![]()
![]()
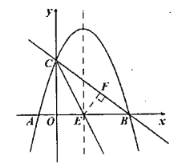
![]() 如图①,过点
如图①,过点![]() 作
作![]() ,垂足为点
,垂足为点![]()
![]()
![]()
![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
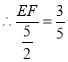
![]()
![]()
![]()
![]() 是的
是的![]() 角平分线
角平分线
![]() 存在
存在
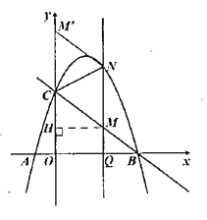
如图②,由题意,得![]()
![]()
![]() ,
,
![]()
![]()
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]()
将![]() 代入
代入
得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 点
点![]()
![]()
![]()
![]() 点
点![]() 落在
落在![]() 轴的正半轴上
轴的正半轴上
![]() 点
点![]() 在直线
在直线![]() 上方
上方
![]()
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
![]()
![]()
![]()
![]()
解得![]() (舍弃),
(舍弃),![]()
![]()

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目