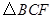题目内容
如图,在平行四边形中,过点A分别作AE⊥BC于点E,AF⊥CD于点
F.
(1)求证:∠BAE=∠DAF;
(2)若AE=4,AF=,
,求CF的长.
证明:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D.
又AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD.
∴∠BAE=∠DAF.------- --2分
(2)在Rt△ABE中,sin∠BAE=,AE=4,可求 AB=5. ---------3分
又∵∠BAE=∠DAF,
∴ sin∠DAF=sin∠BAE=.
在Rt△ADF中,AF=, sin∠DAF =
,可求DF=
-------4分
∵ CD=AB=5.
∴CF=5-=
. …………………………………………5分
解析:略

练习册系列答案
相关题目
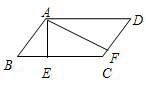 19、如图,在平行四边形中,AE⊥BC于E,AF⊥CD于F,∠EAF=60°,求平行四边形各个内角的度数.
19、如图,在平行四边形中,AE⊥BC于E,AF⊥CD于F,∠EAF=60°,求平行四边形各个内角的度数.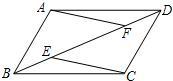 22、如图,在平行四边形中,点E,F是对角线BD上两点,且BF=DE.
22、如图,在平行四边形中,点E,F是对角线BD上两点,且BF=DE. (2013•宜春模拟)如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线将剩下图形的面积平分.(保留作图痕迹)
(2013•宜春模拟)如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线将剩下图形的面积平分.(保留作图痕迹)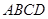 中,以点
中,以点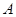 为圆心,
为圆心,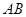 为半径的圆,交
为半径的圆,交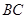 于点
于点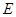 .
.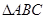 ≌
≌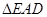 ;
;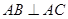 ,
,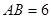 ,
,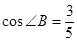 ,求
,求 的长.
的长.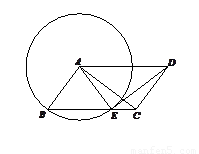
 中,
中,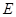 为
为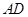 的中点,
的中点,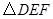 的周长为1,则
的周长为1,则