题目内容
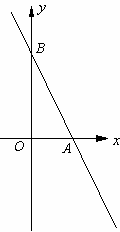
直线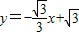 分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.
分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.(1)求A、B、C三点坐标;
(2)求经过O、C、A三点的抛物线解析式;
(3)试判断四边形BOCA的形状并证明;
(4)直线AB上是否存在点P,使得△COP的周长最小?若存在,请求出P点坐标;若不存在,请说明理由.
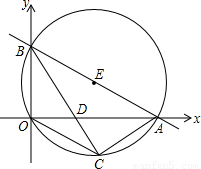
【答案】分析:(1)由直线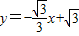 分别与x轴、y轴交于A、B两点,即可求得点A与点B的坐标,然后连接EC,交x轴于点H,由∠COD=∠CBO,根据垂径定理的即可求得OH与AH的长,由勾股定理,可求得AB的长,EH的长,继而求得点C的坐标;
分别与x轴、y轴交于A、B两点,即可求得点A与点B的坐标,然后连接EC,交x轴于点H,由∠COD=∠CBO,根据垂径定理的即可求得OH与AH的长,由勾股定理,可求得AB的长,EH的长,继而求得点C的坐标;
(2)利用待定系数法即可求得经过O、C、A三点的抛物线解析式;
(3)由特殊角的三角函数值,可求得∠OAB与∠COD的度数,然后由圆周角定理,证得OB=AC,∠OCB=∠ABC=30°,即可证得OC∥AB,则可得四边形BOCA的形状是等腰梯形;
(4)由OC已知,可得当OP+CP最小时,△COP的周长最小;过点O作OF⊥AB于点F,并延长交⊙O于点K,连接CK交直线AB于点P,此点即为所求;易证得CK是直径,则可得点P与点E重合,继而求得P点坐标.
解答: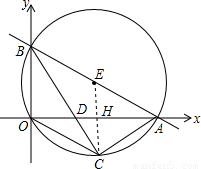 (1)解:∵直线
(1)解:∵直线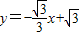 分别与x轴、y轴交于A、B两点,
分别与x轴、y轴交于A、B两点,
∴当x=0时,y=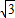 ,当y=0时,x=3,
,当y=0时,x=3,
∴点A(3,0),点B(0,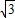 ),
),
∴AB=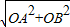 =2
=2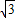 ,
,
∴AE=BE= AB=
AB=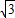 ,
,
连接EC,交x轴于点H,
∵∠COD=∠CBO,
∴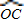 =
=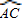 ,
,
∴EC⊥OA,OC=AC,
∴OH=AH= OA=
OA= ,
,
在Rt△AEH中,EH= =
=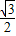 ,
,
∴CH=EC-EH=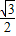 ,
,
∴点C的坐标为:( ,-
,-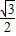 );
);
(2)解:设经过O、C、A三点的抛物线的解析式为y=ax(x-3).
∵点C的坐标为:( ,-
,-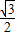 );
);
∴-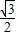 =a×
=a× ×(
×( -3),
-3),
解得:a=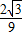 ,
,
∴经过O、C、A三点的抛物线的解析式为:y=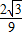 x2-
x2-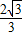 x;
x;
(3)四边形BOCA的形状是等腰梯形.
证明:在Rt△AOB中,tan∠OAB= =
=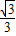 ,
,
∴∠OAB=30°,
在Rt△OCH中,tan∠COH中,tan∠COD=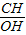 =
= ,
,
∴∠COD=30°,
∴∠OAB=∠COD,
∴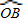 =
= ,
,
∴OC=AC=2CH=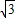 ,
,
∴OC=AC=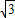 ≠AB,
≠AB,
∵∠ABC=∠COD=30°,∠OCB=∠OAB=30°,
∴∠ABC=∠OCB,
∴OC∥AB,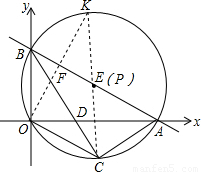
∴四边形BOCA的形状是等腰梯形.
(4)解:存在.
∵OC=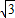 ,
,
∴当OP+CP最小时,△COP的周长最小,
过点O作OF⊥AB于点F,并延长交⊙O于点K,连接CK交直线AB于点P,此点即为所求;
∵∠OAB=30°,
∴∠AOF=60°,
∵∠COD=30°,
∴∠COK=90°,
∴CK是直径,
∵点P在直线AB上,
∴点P于点E重合;
∵点E的横坐标为: ,
,
∴y=-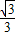 ×
× +
+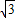 =
=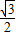 ,
,
∴点P的坐标为:( ,
,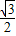 ).
).
点评:此题考查了一次函数的性质、待定系数法求二次函数的解析式、垂径定理、圆周角定理以及等腰梯形的判定等知识.此题综合性较强,难度较大,注意掌握数形结合思想与方程思想的应用.
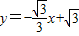 分别与x轴、y轴交于A、B两点,即可求得点A与点B的坐标,然后连接EC,交x轴于点H,由∠COD=∠CBO,根据垂径定理的即可求得OH与AH的长,由勾股定理,可求得AB的长,EH的长,继而求得点C的坐标;
分别与x轴、y轴交于A、B两点,即可求得点A与点B的坐标,然后连接EC,交x轴于点H,由∠COD=∠CBO,根据垂径定理的即可求得OH与AH的长,由勾股定理,可求得AB的长,EH的长,继而求得点C的坐标;(2)利用待定系数法即可求得经过O、C、A三点的抛物线解析式;
(3)由特殊角的三角函数值,可求得∠OAB与∠COD的度数,然后由圆周角定理,证得OB=AC,∠OCB=∠ABC=30°,即可证得OC∥AB,则可得四边形BOCA的形状是等腰梯形;
(4)由OC已知,可得当OP+CP最小时,△COP的周长最小;过点O作OF⊥AB于点F,并延长交⊙O于点K,连接CK交直线AB于点P,此点即为所求;易证得CK是直径,则可得点P与点E重合,继而求得P点坐标.
解答:
 (1)解:∵直线
(1)解:∵直线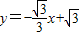 分别与x轴、y轴交于A、B两点,
分别与x轴、y轴交于A、B两点,∴当x=0时,y=
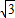 ,当y=0时,x=3,
,当y=0时,x=3,∴点A(3,0),点B(0,
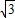 ),
),∴AB=
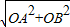 =2
=2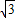 ,
,∴AE=BE=
 AB=
AB=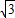 ,
,连接EC,交x轴于点H,
∵∠COD=∠CBO,
∴
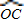 =
=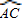 ,
,∴EC⊥OA,OC=AC,
∴OH=AH=
 OA=
OA= ,
,在Rt△AEH中,EH=
 =
=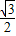 ,
,∴CH=EC-EH=
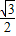 ,
,∴点C的坐标为:(
 ,-
,-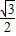 );
);(2)解:设经过O、C、A三点的抛物线的解析式为y=ax(x-3).
∵点C的坐标为:(
 ,-
,-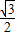 );
);∴-
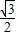 =a×
=a× ×(
×( -3),
-3),解得:a=
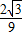 ,
,∴经过O、C、A三点的抛物线的解析式为:y=
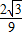 x2-
x2-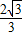 x;
x;(3)四边形BOCA的形状是等腰梯形.
证明:在Rt△AOB中,tan∠OAB=
 =
=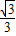 ,
,∴∠OAB=30°,
在Rt△OCH中,tan∠COH中,tan∠COD=
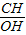 =
= ,
,∴∠COD=30°,
∴∠OAB=∠COD,
∴
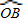 =
=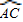 ,
,∴OC=AC=2CH=
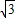 ,
,∴OC=AC=
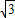 ≠AB,
≠AB,∵∠ABC=∠COD=30°,∠OCB=∠OAB=30°,
∴∠ABC=∠OCB,
∴OC∥AB,

∴四边形BOCA的形状是等腰梯形.
(4)解:存在.
∵OC=
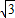 ,
,∴当OP+CP最小时,△COP的周长最小,
过点O作OF⊥AB于点F,并延长交⊙O于点K,连接CK交直线AB于点P,此点即为所求;
∵∠OAB=30°,
∴∠AOF=60°,
∵∠COD=30°,
∴∠COK=90°,
∴CK是直径,
∵点P在直线AB上,
∴点P于点E重合;
∵点E的横坐标为:
 ,
,∴y=-
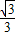 ×
× +
+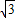 =
=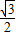 ,
,∴点P的坐标为:(
 ,
,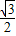 ).
).点评:此题考查了一次函数的性质、待定系数法求二次函数的解析式、垂径定理、圆周角定理以及等腰梯形的判定等知识.此题综合性较强,难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 已知:如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
已知:如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( ) B,⊙P经过点A、点B(圆心P在x轴负半轴上),已知AB=10,
B,⊙P经过点A、点B(圆心P在x轴负半轴上),已知AB=10, (2012•青浦区二模)如图,直线y=x+1分别与 x轴、y轴分别相交于点A、B.抛物线y=ax2+bx+c(a≠0)与 y轴的正半轴相交于点C,与这个一次函数的图象相交于A、D,且sin∠ACB=
(2012•青浦区二模)如图,直线y=x+1分别与 x轴、y轴分别相交于点A、B.抛物线y=ax2+bx+c(a≠0)与 y轴的正半轴相交于点C,与这个一次函数的图象相交于A、D,且sin∠ACB=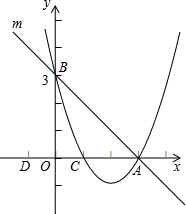 (2013•澄江县二模)如图,已知:直线m分别与x轴、y轴相交于A、B两点,抛物线y=ax2+bx+c经过A(3,0)、B(0,3)、C(1,0)三点.
(2013•澄江县二模)如图,已知:直线m分别与x轴、y轴相交于A、B两点,抛物线y=ax2+bx+c经过A(3,0)、B(0,3)、C(1,0)三点.