题目内容
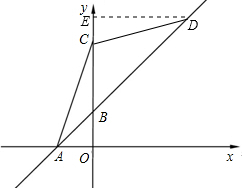
 (2012•青浦区二模)如图,直线y=x+1分别与 x轴、y轴分别相交于点A、B.抛物线y=ax2+bx+c(a≠0)与 y轴的正半轴相交于点C,与这个一次函数的图象相交于A、D,且sin∠ACB=
(2012•青浦区二模)如图,直线y=x+1分别与 x轴、y轴分别相交于点A、B.抛物线y=ax2+bx+c(a≠0)与 y轴的正半轴相交于点C,与这个一次函数的图象相交于A、D,且sin∠ACB=
| ||
| 10 |
(1)求点A、B、C的坐标;
(2)如果∠CDB=∠ACB,求抛物线y=ax2+bx+c的解析式.
分析:(1)设一次函数中的y=0,求出x的值,即A的横坐标,设x=0,求出y的值即B的纵坐标,再利用已知条件和勾股定理求出OC的长,即C的纵坐标;
(2)因为如果∠CDB=∠ACB,则D点的位置不确定,因此小题需要分①当点D在AB延长线上时,②当点D在射线BA上时,两种情况讨论,求出满足题意的抛物线y=ax2+bx+c的解析式即可.
(2)因为如果∠CDB=∠ACB,则D点的位置不确定,因此小题需要分①当点D在AB延长线上时,②当点D在射线BA上时,两种情况讨论,求出满足题意的抛物线y=ax2+bx+c的解析式即可.
解答:解:(1)设一次函数中的y=0,即y=x+1=0,
∴x=-1,
∴点A的坐标(-1,0),
设x=0,即y=1,
∴点B的坐标(0,1),
∵OA=1,在Rt△AOC中,sin∠ACB=
=
,AC=
,
∴OC=
=
=3,
∴点C的坐标(0,3).
(2)
①当点D在AB延长线上时,
∵B(0,1),
∴BO=1,∴AB=
=
,
∵∠CDB=∠ACB,∠BAC=∠CAD,
∴△ABC∽△ACD.
∴
=
,
∴
=
,
∴AD=5
,
过点D作DE⊥y轴,垂足为E,
∵DE∥AO,
∵AD=5
,AB=
,
∴BD=4
,
又∵△BED是等腰直角三角形,
∴BE=DE=4,
∴OE=5,
∴点D的坐标为(4,5).
因为二次函数的解析式为y=ax2+bx+3,
∴
∴
,
∴二次函数解析式为y=-
x2+
x+3;
②当点D在射线BA上时,同理可求得点D(-2,-1),
二次函数解析式为y=x2+4x+3;
综上可知:如果∠CDB=∠ACB,则抛物线的解析式为y=-
x2+
x+3或y=x2+4x+3.
∴x=-1,
∴点A的坐标(-1,0),
设x=0,即y=1,
∴点B的坐标(0,1),
∵OA=1,在Rt△AOC中,sin∠ACB=
| AO |
| AC |
| ||
| 10 |
| 10 |
∴OC=
| AC2-AO2 |
| 10-1 |
∴点C的坐标(0,3).
(2)
①当点D在AB延长线上时,
∵B(0,1),
∴BO=1,∴AB=
| AO2+BO2 |
| 2 |

∵∠CDB=∠ACB,∠BAC=∠CAD,
∴△ABC∽△ACD.
∴
| AD |
| AC |
| AC |
| AB |
∴
| AD | ||
|
| ||
|
∴AD=5
| 2 |
过点D作DE⊥y轴,垂足为E,
∵DE∥AO,
∵AD=5
| 2 |
| 2 |
∴BD=4
| 2 |
又∵△BED是等腰直角三角形,
∴BE=DE=4,
∴OE=5,
∴点D的坐标为(4,5).
因为二次函数的解析式为y=ax2+bx+3,
∴
|
∴
|
∴二次函数解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
②当点D在射线BA上时,同理可求得点D(-2,-1),
二次函数解析式为y=x2+4x+3;
综上可知:如果∠CDB=∠ACB,则抛物线的解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查一次函数和坐标轴的交点问题、二次函数解析式的确定、相似三角形的判定、相似三角形的性质、勾股定理的运用及综合应用知识、解决问题的能力,题目难度不小,对学生的解题能力要求很高.

练习册系列答案
相关题目