题目内容
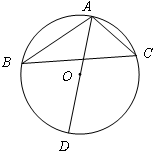
如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE//CD,交AC的延长线于点E,连接BC.

(1)求证:BE为⊙O的切线;
(2)若CD=6,tan∠BCD= ,求⊙O的直径.
,求⊙O的直径.

(1)求证:BE为⊙O的切线;
(2)若CD=6,tan∠BCD=
 ,求⊙O的直径.
,求⊙O的直径.(1)由BC∥CD,AB⊥CD,可证AB⊥BE,从而可证BE为⊙O的切线;(2)7.5
试题分析:(1)由BC∥CD,AB⊥CD,可证AB⊥BE,从而可证BE为⊙O的切线;
(2)由垂径定理知:CM=
 CD,在Rt△BCM中,已知tan∠BCD和CM的值,可将BM,CM的值求出,由弧BC=弧BD,可知:∠BAC=∠BCD,在Rt△ACM中,根据三角函数可将AM的值求出,故⊙O的直径为AB=AM+BM.
CD,在Rt△BCM中,已知tan∠BCD和CM的值,可将BM,CM的值求出,由弧BC=弧BD,可知:∠BAC=∠BCD,在Rt△ACM中,根据三角函数可将AM的值求出,故⊙O的直径为AB=AM+BM.(1)∵BE∥CD,AB⊥CD,
∴AB⊥BE.
∵AB是⊙O的直径,
∴BE为⊙O的切线;
(2)∵AB是⊙O的直径,AB⊥CD,
∴CM=
 CD,弧BC=弧BD,CM=
CD,弧BC=弧BD,CM= CD=3,
CD=3,∴∠BAC=∠BCD.
∵tan∠BCD=
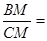
 ,
,∴BM=
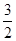 ,
,∵
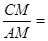 tan∠BCD=
tan∠BCD= .
.∴AM=6.
∴AB=AM+BM=7.5.
点评:本题知识点多,综合性强,是中考常见题,一般难度不大,熟练掌握解直角三角形的运算能力是解题的关键.

练习册系列答案
相关题目
 中,
中, ,
, .
. 是
是 的中点,⊙
的中点,⊙ 与点
与点 .与
.与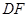 并延长交
并延长交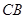 的延长线于点
的延长线于点 .若
.若 ,则
,则 __.
__.
 的半径为5,
的半径为5, 为⊙
为⊙ ⊥
⊥ .若
.若 ,则
,则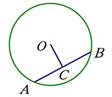
 在同一条直线上,则阴影部分的面积是 .
在同一条直线上,则阴影部分的面积是 .




 ,
, ,则
,则 的长度是 .
的长度是 .