题目内容
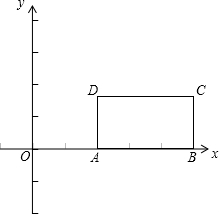 已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y=
已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y= x-1经过这两个顶点中的一个.
x-1经过这两个顶点中的一个.
(1)求出矩形的顶点A、B、C、D的坐标;
(2)以AB为直径作⊙M,经过A、B两点的抛物线,y=ax2+bx+c的顶点是P点.
①若点P位于⊙M外侧且在矩形ABCD内部,求a的取值范围;
②过点C作⊙M的切线交AD于F点,当PF∥AB时,试判断抛物线与y轴的交点Q是位于直线y= x-1的上方?还是下方?还是正好落在此直线上?并说明理由.
x-1的上方?还是下方?还是正好落在此直线上?并说明理由.
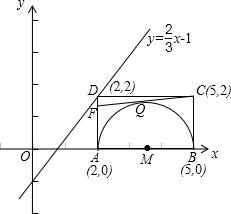 解:(1)如图,建立平面直角坐标系,
解:(1)如图,建立平面直角坐标系,∵矩形ABCD中,AB=3,AD=2,
设A(m,0)(m>0),则有B(m+3,0);C(m+3,2),D(m,2);
若C点过y=
 x-1;则2=
x-1;则2= (m+3)-1,
(m+3)-1,m=-1与m>0不合;
∴C点不过y=
 x-1;
x-1;若点D过y=
 x-1,则2=
x-1,则2= m-1,m=2,
m-1,m=2,∴A(2,0),B(5,0),C(5,2),D(2,2);
(2)①∵⊙M以AB为直径,
∴M(
 ,0),
,0),由于y=ax2+bx+c过A(2,0)和B(5,0)两点,
∴
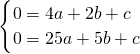 ,
,∴
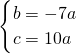 ,
,∴y=ax2-7ax+10a
(也可得:y=a(x-2)(x-5)=a(x2-7x+10)=ax2-7ax+10a)
∴y=a(x-
 )2-
)2- a;
a;∴抛物线顶点P(
 ,-
,- a)
a)∵顶点同时在⊙M内和在矩形ABCD内部,
∴
 <-
<- a<2,
a<2,∴-
 <a<-
<a<- .
.②设切线CF与⊙M相切于Q,交AD于F,设AF=n,n>0;
∵AD、BC、CF均为⊙M切线,
∴CF=n+2,DF=2-n;在Rt△DCF中,
∵DF2+DC2=CF2;
∴32+(2-n)2=(n+2)2,
∴n=
 ,
,∴F(2,
 )
)∴当PF∥AB时,P点纵坐标为
 ;
;∴-
 a=
a= ,
,∴a=-
 ;
;∴抛物线的解析式为:y=-
 x2+
x2+ x-5,
x-5,抛物线与y轴的交点为Q(0,-5),
又直线y=
 x-1与y轴交点(0,-1);
x-1与y轴交点(0,-1);∴Q在直线y=
 x-1下方.
x-1下方.分析:(1)首先建立平面直角坐标系,由矩形ABCD中,AB=3,AD=2,设A(m,0)(m>0),则有B(m+3,0);C(m+3,2),D(m,2);然后若C点过y=
 x-1与C点不过y=
x-1与C点不过y= x-1分析,即可求得矩形的顶点A、B、C、D的坐标;
x-1分析,即可求得矩形的顶点A、B、C、D的坐标;(2)⊙M以AB为直径,即可求得M点的坐标,又由y=ax2+bx+c过A(2,0)和B(5,0)两点,利用待定系数法即可求得二次函数的图象,然后顶点同时在⊙M内和在矩形ABCD内部,即可求得a的取值范围;
②首先设切线CF与⊙M相切于Q,交AD于F,设AF=n,n>0;由AD、BC、CF均为⊙M切线,求得CF与DF的长;在Rt△DCF中,由勾股定理求得n的值,可得F的坐标,然后由当PF∥AB时,求得抛物线的解析式与抛物线与y轴的交点Q的坐标,则可得Q在直线y=
 x-1下方.
x-1下方.点评:此题考查了待定系数法求二次函数的解析式,矩形的性质,勾股定理的应用以及点与函数的关系等知识.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 已知:矩形ABCD,对角线AC、BD相交于点O.
已知:矩形ABCD,对角线AC、BD相交于点O.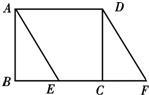 如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.
如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF. 已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).
已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).
 已知:矩形ABCD中,对角线AC与BD交于点O,CE平分∠BCD,交AB于点E,∠OCE=15°,求∠BEO的度数.
已知:矩形ABCD中,对角线AC与BD交于点O,CE平分∠BCD,交AB于点E,∠OCE=15°,求∠BEO的度数.