题目内容
 已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).
已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).(1)求证:BM=DN;
(2)如图②,四边形AMNE是由四边形CMND沿MN翻折得到的,连接CN,求证:四边形AMCN是菱形;
(3)在(2)的条件下,若△CDN的面积与△CMN的面积比为1:3,求
| MN | DN |
分析:(1)连接BD,可证明△OBM≌△ODN,则BM=DN;
(2)先证明四边形AMCN是平行四边形,再由翻折得,AM=CM,则四边形AMCN是菱形;
(3)又S△CDN:S△CMN=1:3,可得DN:CM=1:3,设DN=k,则CN=CM=3k,过N作NG⊥MC于点G,则可求出NG和MN,从而求出比值.
(2)先证明四边形AMCN是平行四边形,再由翻折得,AM=CM,则四边形AMCN是菱形;
(3)又S△CDN:S△CMN=1:3,可得DN:CM=1:3,设DN=k,则CN=CM=3k,过N作NG⊥MC于点G,则可求出NG和MN,从而求出比值.
解答: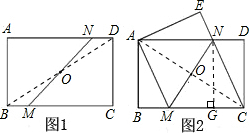 (1)证法一:连接BD,则BD过点O,
(1)证法一:连接BD,则BD过点O,
∵AD∥BC,
∴∠OBM=∠ODN,
又OB=OD,∠BOM=∠DON,
∴△OBM≌△ODN,
∴BM=DN;
证法二:∵矩形ABCD是中心对称图形,点O是对称中心,
∴B、D和M、N关于O点中心对称,
∴BM=DN;
(2)证法一:
∵矩形ABCD,
∴AD∥BC,AD=BC,
又BM=DN,
∴AN=CM,
∴四边形AMCN是平行四边形,
由翻折得,AM=CM,
∴四边形AMCN是菱形;
证法二:由翻折得,AE=CD,∠E=∠D,∠AMN=∠CMN,
又∵∠ANE=∠CND,
∴△ANE≌△CND,
∴AN=CN.
∵AD∥BC,
∴∠ANM=∠CMN,
∴∠AMN=∠ANM,
∴AM=AN,
∴AM=MC=CN=NA,
∴四边形AMCN是菱形.
(3)解法一:∵S△CDN=
DN•CD,S△CMN=
CM•CD,
又S△CDN:S△CMN=1:3,
∴DN:CM=1:3,
设DN=k,则CN=CM=3k,
过N作NG⊥MC于点G,
则CG=DN=k,MG=CM-CG=2k,
NG=
=
=2
k,
∴MN=
=
=2
k,
∴
=
=2
;
解法二:∵S△CDN=
DN•CD,S△CMN=
CM•CD,
又S△CDN:S△CMN=1:3,
∴DN:CM=1:3,
连接AC,则AC过点O,且AC⊥MN,
设DN=k,则CN=AN=CM=3k,AD=4k,
CD=
=
=2
k,
OC=
AC=
=
=
k,
∴MN=2ON=2
=2
=2
k,
∴
=
=2
.
 (1)证法一:连接BD,则BD过点O,
(1)证法一:连接BD,则BD过点O,∵AD∥BC,
∴∠OBM=∠ODN,
又OB=OD,∠BOM=∠DON,
∴△OBM≌△ODN,
∴BM=DN;
证法二:∵矩形ABCD是中心对称图形,点O是对称中心,
∴B、D和M、N关于O点中心对称,
∴BM=DN;
(2)证法一:
∵矩形ABCD,
∴AD∥BC,AD=BC,
又BM=DN,
∴AN=CM,
∴四边形AMCN是平行四边形,
由翻折得,AM=CM,

∴四边形AMCN是菱形;
证法二:由翻折得,AE=CD,∠E=∠D,∠AMN=∠CMN,
又∵∠ANE=∠CND,
∴△ANE≌△CND,
∴AN=CN.
∵AD∥BC,
∴∠ANM=∠CMN,
∴∠AMN=∠ANM,
∴AM=AN,
∴AM=MC=CN=NA,
∴四边形AMCN是菱形.
(3)解法一:∵S△CDN=
| 1 |
| 2 |
| 1 |
| 2 |
又S△CDN:S△CMN=1:3,
∴DN:CM=1:3,
设DN=k,则CN=CM=3k,
过N作NG⊥MC于点G,
则CG=DN=k,MG=CM-CG=2k,
NG=
| CN2-CG2 |
| 9k2-k2 |
| 2 |
∴MN=
| MG2+NG2 |
| 4k2+8k2 |
| 3 |
∴
| MN |
| DN |
2
| ||
| k |
| 3 |
解法二:∵S△CDN=
| 1 |
| 2 |
| 1 |
| 2 |
又S△CDN:S△CMN=1:3,
∴DN:CM=1:3,
连接AC,则AC过点O,且AC⊥MN,
设DN=k,则CN=AN=CM=3k,AD=4k,
CD=
| NC2-DN2 |
| 9k2-k2 |
| 2 |
OC=
| 1 |
| 2 |
| 1 |
| 2 |
| AD2+CD2 |
| 1 |
| 2 |
| 16k2+8k2 |
| 6 |
∴MN=2ON=2
| CN2-OC2 |
| 9k2-6k2 |
| 3 |
∴
| MN |
| DN |
2
| ||
| k |
| 3 |
点评:图形的折叠实际上相当于把折叠部分沿着折痕所在直线作轴对称,所以折叠前后的两个图形是全等三角形,复合的部分就是对应量.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
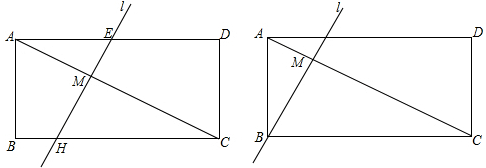
 ,tan∠DAE=
,tan∠DAE= 已知在矩形ABCD中.
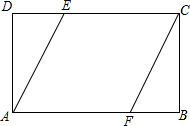
已知在矩形ABCD中. 已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.
已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.