题目内容
(12分)如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
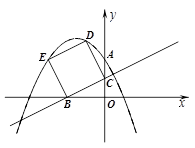
(1)填空:点D的坐标为 ,点E的坐标为 ;
(2)若抛物线y=aa2+ba+c(a≠0)经过A,D,E三点,求该抛物线的解析式;
(3)若正方形和抛物线均以每秒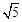 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.
① 在运动过程中,设正方形落在y轴右侧部分的面积为s,求s关于平移时间t(秒)的函数关系式,并写出相应自变量t的取值范围;
② 运动停止时,请直接写出此时的抛物线的顶点坐标.

(1)填空:点D的坐标为 ,点E的坐标为 ;
(2)若抛物线y=aa2+ba+c(a≠0)经过A,D,E三点,求该抛物线的解析式;
(3)若正方形和抛物线均以每秒
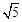 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.① 在运动过程中,设正方形落在y轴右侧部分的面积为s,求s关于平移时间t(秒)的函数关系式,并写出相应自变量t的取值范围;
② 运动停止时,请直接写出此时的抛物线的顶点坐标.
(1)D(﹣1,3)、E(﹣3,2);
(2)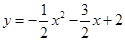 ;
;
(3)①S与x的函数关系式为:当0<t≤ 时,S=5t2,当
时,S=5t2,当 <t≤1时,S=5t﹣
<t≤1时,S=5t﹣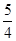 ,当1<t≤
,当1<t≤ 时,S=﹣5t2+15t﹣
时,S=﹣5t2+15t﹣ ;②运动停止时,抛物线的顶点坐标为(
;②运动停止时,抛物线的顶点坐标为( ,
,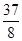 ).
).
(2)
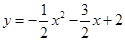 ;
;(3)①S与x的函数关系式为:当0<t≤
 时,S=5t2,当
时,S=5t2,当 <t≤1时,S=5t﹣
<t≤1时,S=5t﹣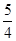 ,当1<t≤
,当1<t≤ 时,S=﹣5t2+15t﹣
时,S=﹣5t2+15t﹣ ;②运动停止时,抛物线的顶点坐标为(
;②运动停止时,抛物线的顶点坐标为( ,
,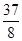 ).
).试题分析:(1)构造全等三角形,由全等三角形对应线段之间的相等关系,求出点D、点E的坐标;
(2)利用待定系数法求出抛物线的解析式;
(3)本问非常复杂,须小心思考与计算:
①为求s的表达式,需要识别正方形(与抛物线)的运动过程.正方形的平移,从开始到结束,总共历时
 秒,期间可以划分成三个阶段:当0<t≤
秒,期间可以划分成三个阶段:当0<t≤ 时,对应图(3)a;当
时,对应图(3)a;当 <t≤1时,对应图(3)b;当1<t≤
<t≤1时,对应图(3)b;当1<t≤ 时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考;
时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考;②当运动停止时,点E到达y轴,点E(﹣3,2)运动到点E′(0,
 ),可知整条抛物线向右平移了3个单位,向上平移了
),可知整条抛物线向右平移了3个单位,向上平移了 个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标.
个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标.试题解析:(1)由题意可知:OB=2,OC=1.
如图(1)所示,过D点作DH⊥y轴于H,过E点作EG⊥x轴于G.
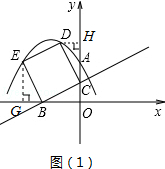
易证△CDH≌△BCO,∴DH=OC=1,CH=OB=2,∴D(﹣1,3);
同理△EBG≌△BCO,∴BG=OC=1,EG=OB=2,∴E(﹣3,2).
∴D(﹣1,3)、E(﹣3,2);
(2)抛物线经过(0,2)、(﹣1,3)、(﹣3,2),
则
 ,解得
,解得 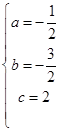 ,
,∴
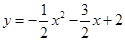 ;
;(3)①当点D运动到y轴上时,t=
 .
.当0<t≤
 时,如图(3)a所示.
时,如图(3)a所示.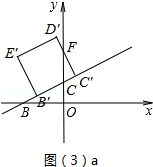
设D′C′交y轴于点F
∵tan∠BCO=
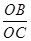 =2,又∵∠BCO=∠FCC′
=2,又∵∠BCO=∠FCC′∴tan∠FCC′=2,即
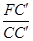 =2
=2∵CC′=
 t,∴FC′=2
t,∴FC′=2 t.
t.∴S△CC′F=
 CC′•FC′=
CC′•FC′=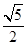 t×
t×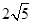 t=5t2
t=5t2当点B运动到点C时,t=1.
当
 <t≤1时,如图(3)b所示.
<t≤1时,如图(3)b所示.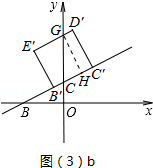
设D′E′交y轴于点G,过G作GH⊥B′C′于H.
在Rt△BOC中,BC=

∴GH=
 ,∴CH=
,∴CH= GH=
GH=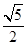
∵CC′=
 t,∴HC′=
t,∴HC′= t﹣
t﹣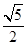 ,∴GD′=
,∴GD′= t﹣
t﹣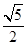
∴S梯形CC′D′G=
 (
( t﹣
t﹣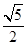 +
+ t)
t) =5t﹣
=5t﹣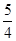
当点E运动到y轴上时,t=
 .
.当1<t≤
 时,如图(3)c所示
时,如图(3)c所示
设D′E′、E′B′分别交y轴于点M、N
∵CC′=
 t,B′C′=
t,B′C′= ,
,∴CB′=
 t﹣
t﹣ ,∴B′N=2CB′=
,∴B′N=2CB′=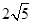 t﹣
t﹣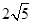
∵B′E′=
 ,∴E′N=B′E′﹣B′N=
,∴E′N=B′E′﹣B′N=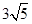 ﹣
﹣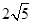 t
t∴E′M=
 E′N=
E′N= (
(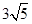 ﹣
﹣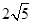 t)
t)∴S△MNE′=
 (
(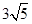 ﹣
﹣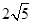 t)•
t)• (
(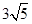 ﹣
﹣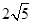 t)=5t2﹣15t+
t)=5t2﹣15t+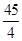
∴S五边形B′C′D′MN=S正方形B′C′D′E′﹣S△MNE′=
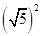 ﹣(5t2﹣15t+
﹣(5t2﹣15t+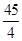 )=﹣5t2+15t﹣
)=﹣5t2+15t﹣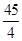
综上所述,S与x的函数关系式为:
当0<t≤
 时,S=5t2,
时,S=5t2,当
 <t≤1时,S=5t﹣
<t≤1时,S=5t﹣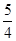 ,
,当1<t≤
 时,S=﹣5t2+15t﹣
时,S=﹣5t2+15t﹣ ;
;②当点E运动到点E′时,运动停止.如图(3)d所示
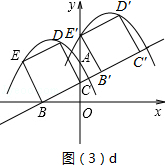
∵∠CB′E′=∠BOC=90°,∠BCO=∠B′CE′
∴△BOC∽△E′B′C
∴

∵OB=2,B′E′=BC=

∴
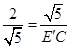
∴CE′=
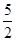
∴OE′=OC+CE′=1+
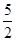 =
=
∴E′(0,
 )
)由点E(﹣3,2)运动到点E′(0,
 ),可知整条抛物线向右平移了3个单位,向上平移了
),可知整条抛物线向右平移了3个单位,向上平移了 个单位.
个单位.∵

∴原抛物线顶点坐标为(
 ,
, )
)∴运动停止时,抛物线的顶点坐标为(
 ,
,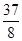 ).
).
练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
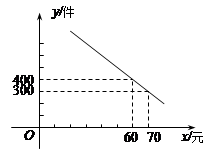
 向左平移2个单位,再向下平移3个单位,得到的抛物线是( )
向左平移2个单位,再向下平移3个单位,得到的抛物线是( )



 向左平移一个单位,所得抛物线的表达式为: .
向左平移一个单位,所得抛物线的表达式为: .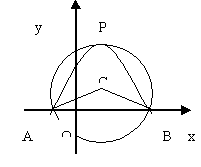

 向右平移一个单位,所得函数解析式为 .
向右平移一个单位,所得函数解析式为 .