题目内容
将一副三角板如下图摆放在一起，连接AD，则∠ADB的正切值为
- A.
- B.
- C.
- D.
D
分析：过点A构造∠ADB所在的直角三角形，设AE为1，得到DE的值，相除即可．
解答：
解：作AE⊥BD，交DB的延长线于点E．
由题意可得：∠ABE=∠CBD=45°，
设AE=1，则AB=
∴BC=
，
∵Rt△BCD是等腰直角三角形，
∴BD=
，
∴DE=1+，
∴tan∠ADB=1÷（+1）=．
故选D．
点评：考查解直角三角形的知识；构造出所求角所在的直角三角形是解决本题的难点．
分析：过点A构造∠ADB所在的直角三角形，设AE为1，得到DE的值，相除即可．
解答：
解：作AE⊥BD，交DB的延长线于点E．由题意可得：∠ABE=∠CBD=45°，
设AE=1，则AB=
∴BC=
，∵Rt△BCD是等腰直角三角形，
∴BD=
，∴DE=1+
，∴tan∠ADB=1÷（
+1）=．故选D．
点评：考查解直角三角形的知识；构造出所求角所在的直角三角形是解决本题的难点．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
小学学习好帮手系列答案
相关题目
如图，线段AB=CD，AB与CD相交于O，且∠AOC=60°，CE是由AB平移所得，则AC+BD与AB的大小关系是
，0.121121112…，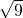
，中，无理数的个数为