题目内容
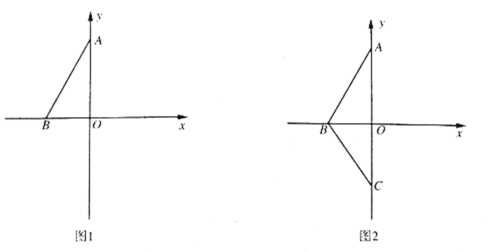
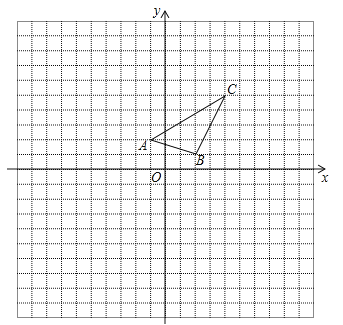
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)以O为中心作出△ABC的中心对称图形△A1B1C1,并写出点B1坐标;
(2)以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.

【答案】(1)点B1坐标为(2,4);(2)点P的坐标为:(1,﹣2).
【解析】
(1) 根据平面直角坐标系可得初始三角形的每个点的坐标, 根据中心对称对称的性质可得对称后的每个点的坐标, 连接起来△A1B1C1,可写出B1坐标.
(2) 由A′的恰好落在△A1B1C1的内部格点上,可求得A′的坐标,由△ABC按顺时针方向旋转90°,可求得P点坐标,可画出旋转后的△A′B′C′。
解:(1)如图所示:
△A1B1C1,即为所求,点B1坐标为(2,4);
(2)如图所示:点P的坐标为:(1,﹣2),
△A′B′C′即为所求.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目