Question

【题目】如图，已知为等边三角形，为上一点，为等边三角形．

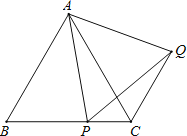
（1）求证：；

（2）与能否互相垂直？若能互相垂直，指出点在上的位置，并给予证明；若与不能垂直，请说明理由．

Answer 1

【答案】（1）见解析；（2）AQ与CQ能互相垂直，此时点P在BC的中点

【解析】

（1）根据等边三角形性质得出AB=AC，AP=AQ，∠BAC=∠B=∠PAQ=60°，求出∠BAP=∠CAQ，根据SAS证△ABP≌△ACQ，推出∠ACQ=∠B=60°=∠BAC，根据平行线的判定推出即可．
（2）根据等腰三角形性质求出∠BAP=30°，求出∠BAQ=90°，根据平行线性质得出∠AQC=90°，即可得出答案．

（1）证明：∵△ABC和△APQ是等边三角形，
∴AB=AC，AP=AQ，∠BAC=∠B=∠PAQ=60°，
∴∠BAP=∠CAQ=60°-∠PAC，
在△ABP和△ACQ中，

，

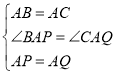∴△ABP≌△ACQ（SAS），
∴∠ACQ=∠B=60°=∠BAC，
∴AB∥CQ；

（2）AQ与CQ能互相垂直，此时点P在BC的中点，
证明：∵当P为BC边中点时，∠BAP=∠BAC=30°，
∴∠BAQ=∠BAP+∠PAQ=30°+60°=90°，
又∵AB∥CQ，
∴∠AQC=90°，
即AQ⊥CQ．