题目内容
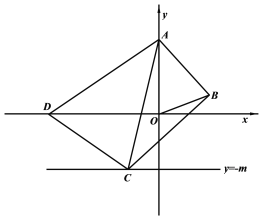
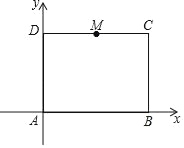
【题目】如图，在平面直角坐标系中有矩形ABCD，A（0，0），C（8，6），M为边CD上一动点，当△ABM是等腰三角形时，M点的坐标为_____．
【答案】（4，6），（8﹣2
，6），（2，6）．
【解析】
分别取三个点作为定点，然后根据勾股定理和等腰三角形的两个腰相等来判断是否存在符合题意的M的坐标．
解：当M为顶点时，AB长为底=8，M在DC中点上，
所以M的坐标为（4， 6），
当B为顶点时，AB长为腰=8，M在靠近D处，根据勾股定理可知ME=
=2
所以M的坐标为（8﹣2，6）；
当A为顶点时，AB长为腰=8，M在靠近C处，根据勾股定理可知MF==2
所以M的坐标为（2，6）；
综上所述，M的坐标为（4，6），（8﹣2，6），（2，6）；
故答案为：（4，6），（8﹣2，6），（2，6）．
练习册系列答案
相关题目
