题目内容
过圆O外一点P向圆作切线，切点分别是A和B，若PA=a，PB=| a+2 |
分析：根据切线长定理列出方程，解方程即可求出a的值，要注意，a为正数．
解答：解：∵PA、PB为圆O切线，
∴PA=PB，
∴
=a，
解得a1=-1（负值舍去），a2=2．
故答案为2．
∴PA=PB，
∴
| a+2 |
解得a1=-1（负值舍去），a2=2．
故答案为2．
点评：本题考查了切线长定理，要知道，从圆外一点引圆的两条切线，它们的切线长相等．
练习册系列答案
相关题目
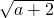，则实数a=________．
，则实数a= ．