题目内容
如图,菱形 的边长为1,
的边长为1,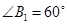 ;作
;作 于点
于点 ,以
,以 为一边,做第二个菱形
为一边,做第二个菱形 ,使
,使 ;作
;作 于点
于点 ,以
,以 为一边做第三个菱形
为一边做第三个菱形 ,使
,使 ;
; 依此类推,这样做的第
依此类推,这样做的第 个菱形
个菱形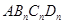 的边
的边
 的长是_____________.
的长是_____________.
 的边长为1,
的边长为1,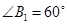 ;作
;作 于点
于点 ,以
,以 为一边,做第二个菱形
为一边,做第二个菱形 ,使
,使 ;作
;作 于点
于点 ,以
,以 为一边做第三个菱形
为一边做第三个菱形 ,使
,使 ;
; 依此类推,这样做的第
依此类推,这样做的第 个菱形
个菱形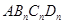 的边
的边 的长是_____________.
的长是_____________.

第一个菱形边长为1,由题得:第二个菱形的边长为 ,第三个菱形的边长为
,第三个菱形的边长为 ,以此类推,第n个菱形的边长为
,以此类推,第n个菱形的边长为 。
。
 ,第三个菱形的边长为
,第三个菱形的边长为 ,以此类推,第n个菱形的边长为
,以此类推,第n个菱形的边长为 。
。
练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 ,
, 是△
是△ 的角平分线.
的角平分线. .
. ∥
∥ ( ).
( ). ( ).
( ). ( ).
( ). ( ).
( ). ( ),
( ),

 , ∠B=90°.
, ∠B=90°.







