题目内容
12.已知直线y=2x+(3-a)与x轴的交点在A(2,0)、B(3,0)之间(包括A、B两点),则a的取值范围是7≤a≤9.分析 根据题意得到x的取值范围是2≤x≤3,则通过解关于x的方程2x+(3-a)=0求得x的值,由x的取值范围来求a的取值范围.
解答 解:∵直线y=2x+(3-a)与x轴的交点在A(2,0)、B(3,0)之间(包括A、B两点),
∴2≤x≤3,
令y=0,则2x+(3-a)=0,
解得x=$\frac{a-3}{2}$,
则2≤$\frac{a-3}{2}$≤3,
解得7≤a≤9.
故答案是:7≤a≤9.
点评 本题考查了一次函数图象上点的坐标特征.根据一次函数解析式与一元一次方程的关系解得x的值是解题的突破口.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
2.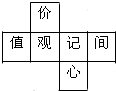 一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
 一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )| A. | 记 | B. | 观 | C. | 心 | D. | 间 |
3.学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
| 选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 73 | 80 | 82 | 83 |
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
20.已知∠α=35°,那么∠α的余角等于( )
| A. | 35° | B. | 55° | C. | 65° | D. | 145° |
17.下列4个数:$\sqrt{9}$、$\frac{22}{7}$、π、($\sqrt{3}$)0,其中无理数是( )
| A. | $\sqrt{9}$ | B. | $\frac{22}{7}$ | C. | π | D. | ($\sqrt{3}$)0 |
16.已知反比例函数y=$\frac{m+1}{x}$,在每一象限内,y随x的增大而减小,则m的取值范围是( )
| A. | m<0 | B. | m<-1 | C. | m>1 | D. | m>-1 |