Question

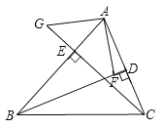
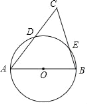
【题目】如图，AB是⊙O的直径，C是⊙O外一点，AC，BC分别与⊙O相交于D．

（1）在图中作出△ABC的边AB上的高CH．（要求：①仅用无刻度真尺，且不能用直尺中的直角；②保留必要的作图痕迹）

（2）连接DE，若，则∠C的度数是　　．

Answer 1

【答案】（1）见解析;（2）60°．

【解析】

（1）连接AE、BD交于点K，连接CK交AB于点H，CH即为所求；（2）证明△DCE∽△BCA，根据相似三角形的性质可得，在Rt△AEC中，可得cos∠C=，由此可求得∠C的度数.

（1）高CH如图所示：

（2）∵∠CDE+∠ADE=180°，∠ADE+∠ABC=180°，

∴∠CDE=∠ABC，∵∠DCE=∠ACB，

∴△DCE∽△BCA，

∴，

∵AB是直径，

∴∠AEC=∠AEB=90°，

∴cos∠C=，

∴∠C=60°，

故答案为60°．