题目内容
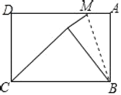
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线![]() 经过点
经过点![]() .
.
![]() 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;
![]() 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点![]() .
.
![]() 若以
若以![]() 为顶点的四边形OBNP是平行四边形时,求m的值.
为顶点的四边形OBNP是平行四边形时,求m的值.
![]() 连接BN,当
连接BN,当![]() 时,求m的值.
时,求m的值.

【答案】(1)![]() ,
,![]() (2)①
(2)①![]() 或
或![]() ②
②![]() 与
与![]()
【解析】试题分析:(1)把A点坐标代入直线解析式可求得k,则可求得B点坐标,由A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)①由M点坐标可表示P、N的坐标,从而可表示出PN的长,根据平行四边形的性质得:OB=PN=2,列方程解出即可;
②有两解,N点在AB的上方或下方,作辅助线,构建等腰直角三角形,由∠PBN=45° 得∠GBP=45°,设GH=BH=t,则由△AHG∽△AOB,得AH=![]() t,GA=
t,GA=![]() ,根据AB=AH+BH=t+
,根据AB=AH+BH=t+![]() t=
t=![]() ,可得BG和BN的解析式,分别与抛物线联立方程组,可得结论.
,可得BG和BN的解析式,分别与抛物线联立方程组,可得结论.
试题解析:解:(1)把A(3,0)代入y=kx+2中得,0=3k+2,k=﹣![]() ,
,
∴直线AB的解析式为:y=﹣![]() x+2,∴B(0,2),把A(3,0)和B(0,2)代入抛物线y=﹣
x+2,∴B(0,2),把A(3,0)和B(0,2)代入抛物线y=﹣![]() x2+bx+c中,则
x2+bx+c中,则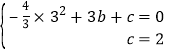 ,解得:
,解得: ,二次函数的表达式为:y=﹣
,二次函数的表达式为:y=﹣![]() ;
;
(2)①如图1,设M(m,0),则P(m,![]() m+2),N(m,﹣
m+2),N(m,﹣![]() )
)
∴PN=yN﹣yP=(﹣![]() )﹣(﹣
)﹣(﹣![]() m+2)=﹣
m+2)=﹣![]() +4m,由于四边形OBNP为平行四边形得PN=OB=2,
+4m,由于四边形OBNP为平行四边形得PN=OB=2,
∴![]() +4m=2,解得:m=
+4m=2,解得:m=![]() 或
或![]()
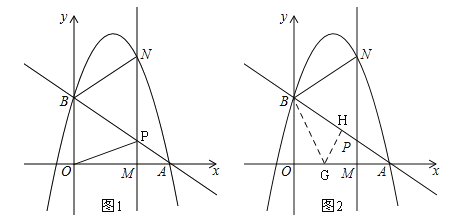
②有两解,N点在AB的上方或下方,如图2,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H.
由∠PBN=45° 得∠GBP=45°,∴GH=BH,设GH=BH=t,则由△AHG∽△AOB,得AH=![]() t,GA=
t,GA=![]() ,由AB=AH+BH=t+
,由AB=AH+BH=t+![]() t=
t=![]() ,解得t=
,解得t=![]() ,∴AG=
,∴AG=![]() ×
×![]() =
=![]() ,从而OG=OA﹣AG=3﹣
,从而OG=OA﹣AG=3﹣![]() =
=![]() ,即G(
,即G(![]() ,0)
,0)
由B(0,2),G(![]() ,0)得:
,0)得:
直线BG:y=﹣5x+2,直线BN:y=0.2x+2.
则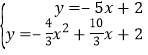 ,解得:x1=0(舍),x2=
,解得:x1=0(舍),x2=![]() ,即m=
,即m=![]() ;
;
则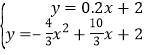 ,解得:x1=0(舍),x2=
,解得:x1=0(舍),x2=![]() ;即m=
;即m=![]() ;
;
故m=![]() 与m=
与m=![]() 为所求.
为所求.

 阅读快车系列答案
阅读快车系列答案