Question

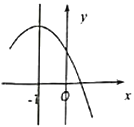
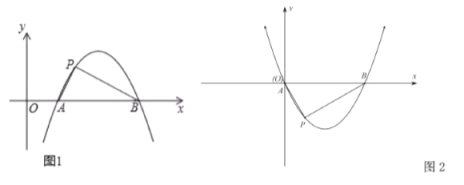
【题目】定义：如图1，抛物线（）与轴交于，两点，点在该抛物线上（点与，两点不重合），如果的三边满足，则称点为抛物线（）的勾股点.

（1）求证：点是抛物线的勾股点.

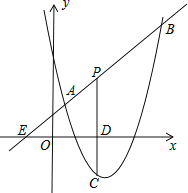
（2）如图2，已知抛物线（）与轴交于，两点，点是抛物线的勾股点，求抛物线的函数表达式.

Answer 1

【答案】(1)见解析；（2）y=

【解析】

（1）先解方程x2-1=0得抛物线与x轴的交点A、B的坐标为（-1，0），B（1，0），利用两点间的距离公式可得到AM2=2，BM2=2，AB2=22=4，则AM2+BM2=AB2，根据题中定义可判断点M（0，-1）是抛物线y=x2-1的勾股点；

（2）作PH⊥AB于H，如图2，先利用P点坐标求出∠PAH=60°，再根据点P（1， ）是抛物线C的勾股点得到∠APB=90°，所以∠PBA=30°，然后计算出BH得到B点坐标，于是可利用待定系数法求抛物线C的解析式．

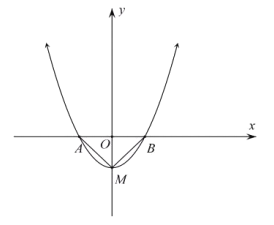
（1）如图所示：令得，，解得

∴，

∴,,,

∴

∴

∴点是抛物线的勾股点.

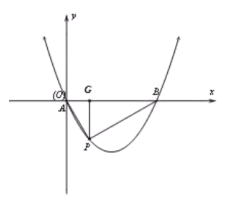
（2）抛物线过原点，即点

如图，作轴于点

∵点的坐标为

∴，，

∵点是抛物线的勾股点

∴

∴是直角三角形

设

∵

∴

∴

∴

∴

∴点坐标为

设

将点代入得：

∴