题目内容
已知a、b、c分别为△ABC的三边长,a=5,且 +(b-c+1)2=0,则△ABC的面积为________.
+(b-c+1)2=0,则△ABC的面积为________.
6
分析:根据非负数的性质,求得三角形的三边,再根据勾股定理的逆定理判断三角形的形状,最后根据三角形的面积公式解答.
解答:∵a、b、c分别为△ABC的三边长,a=5, +(b-c+1)2=0
+(b-c+1)2=0
∴ ,解得
,解得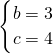 ,
,
∵32+42=52
∴根据勾股定理的逆定理得此三角形为直角三角形.
则△ABC的面积为 bc=
bc= ×3×4=6,故填6.
×3×4=6,故填6.
点评:解答此题的关键是根据已知条件列出方程组,解出b,c的值,判断出三角形的形状,再根据三角形的面积公式解答.
分析:根据非负数的性质,求得三角形的三边,再根据勾股定理的逆定理判断三角形的形状,最后根据三角形的面积公式解答.
解答:∵a、b、c分别为△ABC的三边长,a=5,
 +(b-c+1)2=0
+(b-c+1)2=0∴
 ,解得
,解得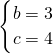 ,
,∵32+42=52
∴根据勾股定理的逆定理得此三角形为直角三角形.
则△ABC的面积为
 bc=
bc= ×3×4=6,故填6.
×3×4=6,故填6.点评:解答此题的关键是根据已知条件列出方程组,解出b,c的值,判断出三角形的形状,再根据三角形的面积公式解答.

练习册系列答案
相关题目