题目内容
在Rt△ABC中,∠C=90°,AC=4,BC=3.
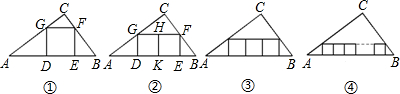
(1)如图①,四边形DEFG为△ABC的内接正方形,则正方形的边长= ;
(2)如图②,三角形内有并排的两个相等的正方形,它们组成的矩形内接于△ABC,则正方形的边长= ;
(3)如图③,三角形内有并排的三个相等的正方形,它们组成的矩形内接于△ABC,则正方形的边长= ;
(4)如图④,三角形内有并排的n个相等的正方形,它们组成的矩形内接于△ABC,则正方形的边长= .
(1)如图①,四边形DEFG为△ABC的内接正方形,则正方形的边长=
(2)如图②,三角形内有并排的两个相等的正方形,它们组成的矩形内接于△ABC,则正方形的边长=
(3)如图③,三角形内有并排的三个相等的正方形,它们组成的矩形内接于△ABC,则正方形的边长=
(4)如图④,三角形内有并排的n个相等的正方形,它们组成的矩形内接于△ABC,则正方形的边长=

考点:相似三角形的判定与性质,正方形的性质
专题:规律型
分析:(1)过C作CM⊥AB交AB于点M,交GF于点N,由条件可求得AB=5,CM=2.4,由GF∥AB可得
=
,设正方形的边长为x,则GF=MN=x,则CN=CM-MN=2.4-x,代入可求得x的值,即得出正方形的边长;
(2)同理可过C作CM⊥AB交AB于点M,交GF于点N,此时设正方形的边长为x,则GF=2x,MN=x,CN=2.4-x,代入可求得x的值;
(3)同(2)可得出GF=3x,CN=2.4-x,代入可求得x的值;
(4)同(2)可得出GF=nx,CN=2.4-x,代入可求得x的值.
| CN |
| CM |
| GF |
| AB |
(2)同理可过C作CM⊥AB交AB于点M,交GF于点N,此时设正方形的边长为x,则GF=2x,MN=x,CN=2.4-x,代入可求得x的值;
(3)同(2)可得出GF=3x,CN=2.4-x,代入可求得x的值;
(4)同(2)可得出GF=nx,CN=2.4-x,代入可求得x的值.
解答: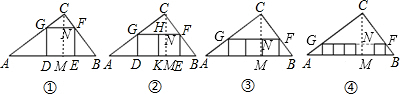 解:(1)如图①,过C作CM⊥AB交AB于点M,交GF于点N,
解:(1)如图①,过C作CM⊥AB交AB于点M,交GF于点N,
∵∠C=90°,AC=4,BC=3,
∴AB=5,CM=2.4,
∵GF∥AB可,
∵
=
,
设正方形的边长为x,则GF=MN=x,CN=CM-MN=2.4-x,
∴
=
,
解得x=
,即正方形的边长为
,
故答案为:
;
(2)如图②,过C作CM⊥AB交AB于点M,交GF于点N,
同理可得GF=2x,CN=2.4-x,
∴
=
,解得x=
,即正方形的边长为
,
故答案为:
;
(3)如图③,过C作CM⊥AB交AB于点M,交GF于点N,
同理可得GF=3x,CN=2.4-x,
∴
=
,解得x=
,即正方形的边长为
,
故答案为:
;
(4)如图④,过C作CM⊥AB交AB于点M,交GF于点N,
同理可得GF=nx,CN=2.4-x,
∴
=
,解得x=
,即正方形的边长为
,
故答案为:
.
 解:(1)如图①,过C作CM⊥AB交AB于点M,交GF于点N,
解:(1)如图①,过C作CM⊥AB交AB于点M,交GF于点N,∵∠C=90°,AC=4,BC=3,
∴AB=5,CM=2.4,
∵GF∥AB可,
∵
| CN |
| CM |
| GF |
| AB |
设正方形的边长为x,则GF=MN=x,CN=CM-MN=2.4-x,
∴
| 2.4-x |
| 2.4 |
| x |
| 5 |
解得x=
| 60 |
| 37 |
| 60 |
| 37 |
故答案为:
| 60 |
| 37 |
(2)如图②,过C作CM⊥AB交AB于点M,交GF于点N,
同理可得GF=2x,CN=2.4-x,
∴
| 2.4-x |
| 2.4 |
| 2x |
| 5 |
| 60 |
| 49 |
| 60 |
| 49 |
故答案为:
| 60 |
| 49 |
(3)如图③,过C作CM⊥AB交AB于点M,交GF于点N,
同理可得GF=3x,CN=2.4-x,
∴
| 2.4-x |
| 2.4 |
| 3x |
| 5 |
| 60 |
| 61 |
| 60 |
| 61 |
故答案为:
| 60 |
| 61 |
(4)如图④,过C作CM⊥AB交AB于点M,交GF于点N,
同理可得GF=nx,CN=2.4-x,
∴
| 2.4-x |
| 2.4 |
| nx |
| 5 |
| 60 |
| 12n+25 |
| 60 |
| 12n+25 |
故答案为:
| 60 |
| 12n+25 |
点评:本题主要考查相似三角形的判定和性质,在(1)中利用条件找到GF和CM之间的比例关系是解题的关键,后面的解题过程可以类比(1)可得到答案.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
一次函数y=2x-4的图象一定经过点( )
| A、(1,2) |
| B、(1,-2) |
| C、(2,4) |
| D、(2,-4) |
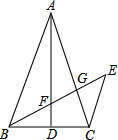 如图,已知△ABC中,AB=AC,D为BC的中点,CE∥AB,BE交AD、AC于E、G,求证:BF2=FG•FE.
如图,已知△ABC中,AB=AC,D为BC的中点,CE∥AB,BE交AD、AC于E、G,求证:BF2=FG•FE.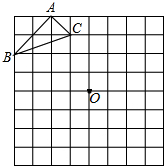 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点),按要求画出下列图形(不写画法,保留作图痕迹).
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点),按要求画出下列图形(不写画法,保留作图痕迹).