题目内容
11．设x2+7x+6=a（x+b）2+c，则c的值为（ ）| A． | -$\frac{31}{3}$ | B． | 6 | C． | -$\frac{25}{4}$ | D． | $\frac{67}{3}$ |
分析 首先把x2+7x+6利用完全平方公式变形得出（x+$\frac{7}{2}$）2-$\frac{25}{4}$，进一步对比得出c的数值即可．
解答 解：∵x2+7x+6
=x2+7x+$\frac{49}{4}$-$\frac{49}{4}$+6
=（x+$\frac{7}{2}$）2-$\frac{25}{4}$
∴c=-$\frac{25}{4}$．
故选：C．
点评 此题考查配方法的运用，掌握完全平方公式是解决问题的关键．
练习册系列答案
相关题目
1．
一条排水管的截面如图所示．已知排水管的水深CD=4，水面宽AB=16，则截面圆半径OB是（ ）
一条排水管的截面如图所示．已知排水管的水深CD=4，水面宽AB=16，则截面圆半径OB是（ ）| A． | 8 | B． | 10 | C． | 12 | D． | $8\sqrt{3}$ |
2．下列运算正确的是（ ）
| A． | （a2）3=a6 | B． | （ab）2=ab2 | C． | a2+a2=a4 | D． | a•a2=a2 |
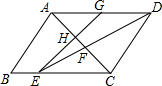如图，已知?ABCD，DE平分∠ADC分别交BC、AC于点E、F，G是AD中点，EG交AC于点H．若AB=4，AD=6．求