题目内容
如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(4,3),O(0,0),B(6,0).点M是OB边上异于O,B的一动点,过点M作MN∥AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点M(x,0),△PMN的面积为S.
(1)求出OA所在直线的解析式,并求出点M的坐标为(1,0)时,点N的坐标;
(2)求出S关于x的函数关系式,写出x的取值范围,并求出S的最大值;
(3)若S:S△ANB=2:3时,求出此时N点的坐标.


解:(1)设直线OA的解析式为y=k1 x,∵A(4,3),
∴3=4k1,解得k1=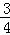 ,
,
∴OA所在的直线的解析式为:y=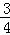 x,
x,
同理可求得直线AB的解析式为;y=﹣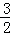 x+9,
x+9,
∵MN∥AB,
∴设直线MN的解析式为y=﹣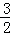 x+b,把M(1,0)代入得:b=
x+b,把M(1,0)代入得:b=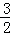 ,
,
∴直线MN的解析式为y=﹣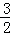 x+
x+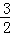 ,
,
解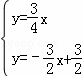 ,得
,得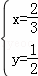 ,
,
∴N(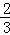 ,
,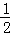 ).
).
(2)如图2,作NH⊥OB于H,AG⊥OB于G,则AG=3.
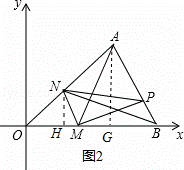
∵MN∥AB,
∴△MBN的面积=△PMN的面积=S,
∴△OMN∽△OBA,
∴NH:AG=OM:OB,
∴NH:3=x:6,即NH=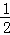 x,
x,
∴S=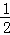 MB•NH=
MB•NH=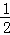 ×(6﹣x)×
×(6﹣x)×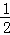 x=﹣
x=﹣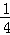 (x﹣3)2+
(x﹣3)2+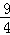 (0<x<6),
(0<x<6),
∴当x=3时,S有最大值,最大值为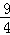 .
.
(3)如图2,∵MN∥AB,
∴△AMB的面积=△ANB的面积=S△ANB,△NMB的面积=△NMP的面积=S
∵S:S△ANB=2:3,
∴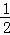 MB•NH:
MB•NH: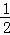 MB•AG=2:3,即NH;AG=2:3,
MB•AG=2:3,即NH;AG=2:3,
∵AG⊥OB于G,NH⊥OB,
∴NH∥AG,
∴ON:OA=NH:AG=2:3,
∵MN∥AB,
∴OM:OB=ON:OA=2:3,
∵OA=6,
∴ =
=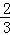 ,
,
∴OM=4,
∴M(4,0)
∵直线AB的解析式为;y=﹣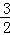 x+9,
x+9,
∴设直线MN的解析式y=﹣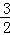 x+b
x+b
∴代入得:0=﹣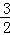 ×4+b,
×4+b,
解得b=6,
∴直线MN的解析式为y=﹣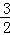 x+6,
x+6,
解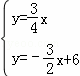 得
得 ,
,
∴N(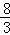 ,2).
,2).


 名校课堂系列答案
名校课堂系列答案如图,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O,则下列判断不正确的是( )
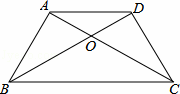
|
| A. | △ABC≌△DCB | B. | △AOD≌△COB | C. | △ABO≌△DCO | D. | △ADB≌△DAC |







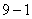 和图
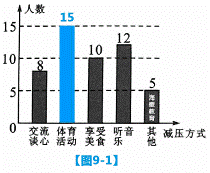
和图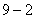 两幅不完整的统计图,请根据统计图中的信息解答下列问题:
两幅不完整的统计图,请根据统计图中的信息解答下列问题: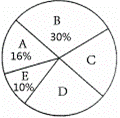


 的解集是
的解集是 
 =
= 的解为
的解为  的解集是( )
的解集是( )