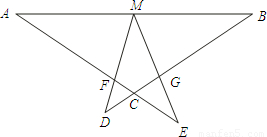
题目内容
已知,如图:∠DME=∠A=∠B=![]() ,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G.
,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G.
(1)求证;△EMF∽△EAM;
(2)连结FG,如果![]() =30°,AB=
=30°,AB=![]() ,AF=5,求FG的长.
,AF=5,求FG的长.

如图,(1)∵∠DME=∠A=∠B=![]() ∠MEF=∠AEM(公共角)
∠MEF=∠AEM(公共角)
∴△EMF与△EAM相似
(2)连结FG、MC,过点F作FK⊥BD,垂足为D,∵∠![]()
∴∠DME=∠A=∠B=30°∴∠ACB=120°,∠FCK=60°
∵M是AB的中点,AB=![]() ∴∠ACM=60°, ∴AC=AB=6
∴∠ACM=60°, ∴AC=AB=6
∠BMG+∠AMF=150°,∠AMF+∠AFM=150°,
∴∠AFM=∠BMG
△BMG与△AFM相似,∴![]()
又∵AF=5,∴![]() ,∴
,∴![]() ,
,
![]() ,FC=6-5=1,所以FK
,FC=6-5=1,所以FK![]() ,CK=
,CK=![]()
![]()


练习册系列答案
相关题目
 已知,如图:∠DME=∠A=∠B=α,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G.
已知,如图:∠DME=∠A=∠B=α,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G.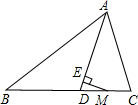 已知:如图,△ABC中,∠ACB>∠ABC,记∠ACB-∠ABC=α,AD为△ABC的角平分线,M为DC上一点,ME与AD所在直线垂直,垂足为E.
已知:如图,△ABC中,∠ACB>∠ABC,记∠ACB-∠ABC=α,AD为△ABC的角平分线,M为DC上一点,ME与AD所在直线垂直,垂足为E.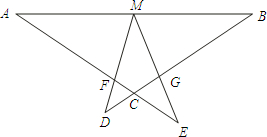 已知,如图:∠DME=∠A=∠B=α,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G.
已知,如图:∠DME=∠A=∠B=α,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G. ,AF=5,求FG的长.
,AF=5,求FG的长.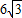 ,AF=5,求FG的长.
,AF=5,求FG的长.