题目内容
已知,如图:∠DME=∠A=∠B=α,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G.(1)求证;△EMF∽△EAM;
(2)连结FG,如果α=30°,AB=
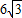 ,AF=5,求FG的长.
,AF=5,求FG的长.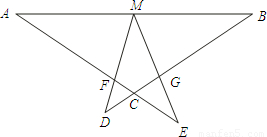
【答案】分析:(1)根据由两对角相等的两个三角形相似即可证明△EMF∽△EAM;
(2)连接FG、MC,过F作FK⊥BD,首先证明△BMG∽△AFM,利用相似的性质可得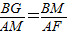 ,因为AF=5,所以,进而求出BG,再求出FK和CK的值,利用勾股定理即可求出GK的值.
,因为AF=5,所以,进而求出BG,再求出FK和CK的值,利用勾股定理即可求出GK的值.
解答:(1)证明:∵∠DME=∠A=∠B=α,∠MEF=∠AEM,
∴△EMF∽△EAM;
(2)解:连接FG、MC,过F作FK⊥BD,
∴∠α=30°,
∴∠DME=∠A=∠B=30°,
∴∠ACB=120°,∠FCK=60°,
∵M为线段AB中点,AB=6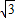 ,
,
∴∠ACM=60°,
∴AC=BC=6,
∵∠BMG+∠AFM=150°,∠AMF+∠AFM=150°,
∴∠AFM=∠BMG,
∴△BMG∽△AFM,
∴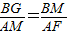 ,
,
∵AF=5,
∴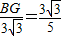 ,
,
∴BG=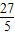 ,
,
∴CG= ,FC=6-5=1,
,FC=6-5=1,
∴FK=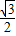 ,CK=
,CK= ,
,
∴GK=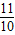 ,
,
∴FG=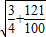 =
= .
.
点评:此题考查了相似三角形的判定与性质、等边三角形的性质与判定以及勾股定理的运用,此题难度适中,注意掌握数形结合思想的应用.
(2)连接FG、MC,过F作FK⊥BD,首先证明△BMG∽△AFM,利用相似的性质可得
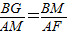 ,因为AF=5,所以,进而求出BG,再求出FK和CK的值,利用勾股定理即可求出GK的值.
,因为AF=5,所以,进而求出BG,再求出FK和CK的值,利用勾股定理即可求出GK的值.解答:(1)证明:∵∠DME=∠A=∠B=α,∠MEF=∠AEM,
∴△EMF∽△EAM;

(2)解:连接FG、MC,过F作FK⊥BD,
∴∠α=30°,
∴∠DME=∠A=∠B=30°,
∴∠ACB=120°,∠FCK=60°,
∵M为线段AB中点,AB=6
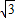 ,
,∴∠ACM=60°,
∴AC=BC=6,
∵∠BMG+∠AFM=150°,∠AMF+∠AFM=150°,
∴∠AFM=∠BMG,
∴△BMG∽△AFM,
∴
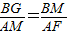 ,
,∵AF=5,
∴
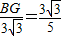 ,
,∴BG=
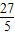 ,
,∴CG=
 ,FC=6-5=1,
,FC=6-5=1,∴FK=
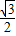 ,CK=
,CK= ,
,∴GK=
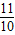 ,
,∴FG=
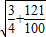 =
= .
.点评:此题考查了相似三角形的判定与性质、等边三角形的性质与判定以及勾股定理的运用,此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图:∠DME=∠A=∠B=α,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G.
已知,如图:∠DME=∠A=∠B=α,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G.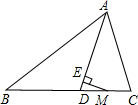 已知:如图,△ABC中,∠ACB>∠ABC,记∠ACB-∠ABC=α,AD为△ABC的角平分线,M为DC上一点,ME与AD所在直线垂直,垂足为E.
已知:如图,△ABC中,∠ACB>∠ABC,记∠ACB-∠ABC=α,AD为△ABC的角平分线,M为DC上一点,ME与AD所在直线垂直,垂足为E.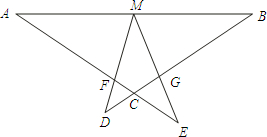 已知,如图:∠DME=∠A=∠B=α,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G.
已知,如图:∠DME=∠A=∠B=α,M为线段AB中点,AE与BD交于C,交MD于F,ME交BD于G. ,AF=5,求FG的长.
,AF=5,求FG的长.