题目内容
17. 如图,已知B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q,则结论:①AE=CD;②CQ=CA;③PQ∥AD;④EP=QD中,其中正确结论是①③④.
如图,已知B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q,则结论:①AE=CD;②CQ=CA;③PQ∥AD;④EP=QD中,其中正确结论是①③④.
分析 由等边三角形的性质可证得△ABE≌△CBD,可求得AE=CD,可判断①;由全等三角形的性质得出∠BAP=∠BCQ,证出∠ABC=∠CBQ=60°,由ASA证明△ABP≌△CBQ,得出CQ=AP≠CA,可判断②;证明△PBQ是等边三角形,得出∠BPQ=60°=∠ABC,由平行线的判定方法得出PQ∥AD,可判断③;由AE=CD,AP=CQ,得出EP=QD,可判断④;可求得答案.
解答 解:
∵△ABC、△BDE均为等边三角形,∴AB=AC=BC,BD=BE,∠ABC=∠EBD=60°,
∴180°-∠EBD=180°-∠ABC,
即∠ABE=∠CBD,
在△ABE与△CBD中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBD}\\{BE=BD}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴AE=CD,故①正确;
∴∠BAP=∠BCQ,
∵∠ABC=∠EBD=60°,
∴∠CBQ=180°-60°×2=60°,
∴∠ABC=∠CBQ=60°,
在△ABP与△CBQ中,
$\left\{\begin{array}{l}{∠BAP=BCQ}\\{AB=CB}\\{∠ABC=∠CBQ}\end{array}\right.$,
∴△ABP≌△CBQ(ASA),
∴CQ=AP≠CA,故②不正确;
∵∠CBQ=60°,BP=BQ,
∴△PBQ是等边三角形,
∴∠BPQ=60°=∠ABC,
∴PQ∥AD,故③正确;
∵AE=CD,AP=CQ,
∴EP=QD,故④正确;
综上可知正确的为①③④,
故答案为:①③④.
点评 本题考查了等边三角形的判定与性质、全等三角形的判定及性质、平行线的判定等知识;本题综合性强,难度不大,证明三角形全等是解决问题的关键.

| A. | (x2)3=x6 | B. | (2x)2=2x2 | C. | (x-y)2=x2-y2 | D. | x2•x3=x6 |
| A. | (4,5) | B. | (-4,5) | C. | (4,-5) | D. | (-4,-5) |
| A. | 系数是-4,次数是5 | B. | 系数是-4π,次数是4 | ||
| C. | 系数是-4,次数是4 | D. | 系数是-4π,次数是3 |
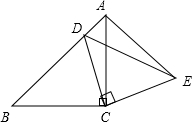 已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,试说明:
已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,试说明: