题目内容
如图所示，在平面直角坐标系xOy中，正方形OABC的边长为2cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线y=ax2+bx+c经过点A、B和
D 
.
（1）求抛物线的解析式.
（2）如果点P由点A出发沿AB边以2cm/s的速度向点B运动，同 时点Q由点B出发沿BC边以1cm/s的速度向点C运动，当其中一点到达终点时，另一点也随之停止运动. 设S=PQ2(cm2)
①试求出S与运动时间t之
间的函数关系式，并写出t的取值范围；
②当S取
时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形? 如果存在，求出R点的坐标；如果不存在，请说明理由.
（3）在抛物线的对称轴上求点M，使得M到D、A的距离之差最大，求出点M的坐标.
解: (1)据题意知: A(0, －2), B(2, －2) ，D（4，—
）,
则 解得
练习册系列答案
相关题目
交于点A，过点A分别作x轴、y轴的垂线，垂足为点B、C．如果四边形OBAC是正方形，求一次函数的关系式．
5、如图所示，在平面直角坐标系中，点A、B的坐标分别为（-2，0）和（2，0）．月牙①绕点B顺时针旋转90°得到月牙②，则点A的对应点A′的坐标为（ ）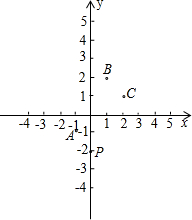
如图所示，在平面直角坐标系中，一颗棋子从点P处开始依次关于点A，B，C作循环对称跳动，即第一次从点P跳到关于点A的对称点M处，第二次从点M跳到关于点B的对称点N处，第三次从点N跳到关于点C的对称点处，…如此下去．
如图所示，在平面直角坐标系xoy中，有一组对角线长分别为1，2，3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2，其对角线OB1、B1B2、B2 B3依次放置在y轴上（相邻顶点重合），依上述排列方式，对角线长为n的第n个正方形的顶点An的坐标为
BE．