Question

【题目】如图，一次函数y=﹣x+b与反比例函数y= （k≠0）的图象相交于A（﹣1，4）、B（4，﹣1）两点，直线l⊥x轴于点E（﹣4，0），与反比例函数和一次函数的图象分别相交于点C、D，连接AC、BC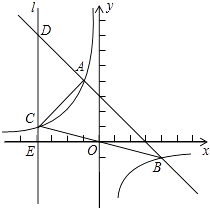

（1）求出b和k；
（2）求证：△ACD是等腰直角三角形；
（3）在y轴上是否存在点P，使S△PBC=S△ABC？若存在，请求出P的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解：∵一次函数y=﹣x+b的图象经过点A（﹣1，4）

∴﹣（﹣1）+b=4，

即b=3，

又∵反比例函数y= （k≠0）的图象经过点A（﹣1，4）

∴k=xy=（﹣1）×4=﹣4；

（2）证明：∵直线l⊥x轴于点E（﹣4，0）则直线l解析式为x=﹣4，

∴直线x=﹣4与一次函数y=﹣x+3交于点D，则D（﹣4，7）

直线x=﹣4与反比例函数y=﹣ 交于点C，

则C（﹣4，1）

过点A作AF⊥直线l于点F，

∵A（﹣1，4），C（﹣4，1），D（﹣4，7）

∴CD=6，AF=3，DF=3，FC=3

又∵∠AFD=∠AFC=90°，

由勾股定理得：AC=AD=3

又∵AD2+AC2= =36

CD2=62=36

∴AD2+AC2=CD2

∴由勾股定理逆定理得：△ACD是直角三角形，

又∵AD=AC

∴△ACD是等腰直角三角形；

（3）解：过点A作AP1∥BC，交y轴于P1，

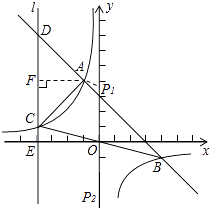
则S△PBC=S△ABC

∵B（4，﹣1），C（﹣4，1）

∴直线BC的解析式为y=﹣ x

∵设直线AP1的解析式为y=﹣ x+b1，把A（﹣1，4）代入可求b1= ，

∴P1（0， ），

∴作P1关于x轴的对称点P2，则 =S△ABC，

故P2（0，﹣ ）；

即存在P1（0， ），P2（0，﹣ ）；

【解析】（1）利用待定系数法即可求解。
（2）根据已知及点E的坐标易求出点C、D的坐标，因此可求出DC的长，过点A作AF⊥直线l于点F，即可求出AF，DF，FC的长，根据垂直平分线的性质得出AC=AD，然后再证明△ACD是直角三角形，即可得出结论。
（3）先求出直线BC的函数解析式，再求出直线AP1的解析式，就可求出点P1的坐标。作P1关于x轴的对称点P2，则S △ P 1 B C = S △ P 2 B C=S△ABC，，就可求出点P2的坐标。
【考点精析】认真审题，首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°)，还要掌握确定一次函数的表达式(确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法)的相关知识才是答题的关键．