Question

【题目】如图，以直角三角形AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足．D为线段AC的中点．在平面直角坐标系中，以任意两点P（x1，y1）、Q（x2，y2）为端点的线段中点坐标为，．

（1）则A点的坐标为　 　；点C的坐标为　 　．D点的坐标为　 　．

（2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．设运动时间为t（t＞0）秒．问：是否存在这样的t，使S△ODP＝S△ODQ，若存在，请求出t的值；若不存在，请说明理由．

（3）点F是线段AC上一点，满足∠FOC＝∠FCO，点G是第二象限中一点，连OG，使得∠AOG＝∠AOF．点E是线段OA上一动点，连CE交OF于点H，当点E在线段OA上运动的过程中，的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．

Answer 1

【答案】（1）（0，4），（2，0），（1，2）；（2）存在，t＝1；（3）的值不变，其值为2．

【解析】

（1）根据绝对值和算术平方根的非负性，求得a，b的值，再利用中点坐标公式即可得出答案；

（2）先得出CP＝t，OP＝2﹣t，OQ＝2t，AQ＝4﹣2t，再根据S△ODP＝S△ODQ，列出关于t的方程，求得t的值即可；

（3）过H点作AC的平行线，交x轴于P，先判定OG∥AC，再根据角的和差关系以及平行线的性质，得出∠PHO＝∠GOF＝∠1+∠2，∠OHC＝∠OHP+∠PHC＝∠GOF+∠4＝∠1+∠2+∠4，最后代入进行计算即可．

解：（1）∵．

∴a﹣2b＝0，b﹣2＝0，

解得a＝4，b＝2，

∴A（0，4），C（2，0）；

∴x＝＝1，y＝＝2，

∴D（1，2）．

故答案为（0，4），（2，0），（1，2）．

（2）如图1中，

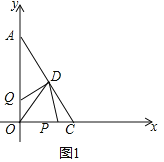
由条件可知：P点从C点运动到O点时间为2秒，Q点从O点运动到A点时间为2秒，

∴0＜t≤2时，点Q在线段AO上，

即 CP＝t，OP＝2﹣t，OQ＝2t，AQ＝4﹣2t，

∴S△DOP＝OPyD＝（2﹣t）×2＝2﹣t，S△DOQ＝OQxD＝×2t×1＝t，

∵S△ODP＝S△ODQ，

∴2﹣t＝t，

∴t＝1；

（3）的值不变，其值为2．理由如下：如图2中，

∵∠2+∠3＝90°，

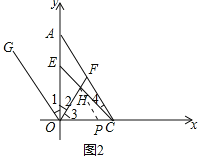
又∵∠1＝∠2，∠3＝∠FCO，

∴∠GOC+∠ACO＝180°，

∴OG∥AC，

∴∠1＝∠CAO，

∴∠OEC＝∠CAO+∠4＝∠1+∠4，

如图，过H点作AC的平行线，交x轴于P，则∠4＝∠PHC，PH∥OG，

∴∠PHO＝∠GOF＝∠1+∠2，

∴∠OHC＝∠OHP+∠PHC＝∠GOF+∠4＝∠1+∠2+∠4，

∴＝，

＝，

＝2．