题目内容
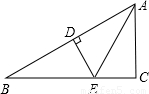
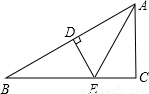
已知：BE平分∠ABC，DE∥BC，F为BE中点，试说明：DF⊥BE．
证明：∵BE平分∠ABC，∴∠ABE=∠FBC，
∵DE∥BC，∴∠DEB=∠EBC，
∴∠ABE=∠DEB，∴BD=DE，
∵F为BE中点，∴DF⊥BE．
分析：要使DF⊥BE．因为F为BE中点，所以只需证明BD=DE即可．
点评：本题综合考查了平行线和角平分线的性质，等腰三角形的性质及判定．
∵DE∥BC，∴∠DEB=∠EBC，
∴∠ABE=∠DEB，∴BD=DE，
∵F为BE中点，∴DF⊥BE．
分析：要使DF⊥BE．因为F为BE中点，所以只需证明BD=DE即可．
点评：本题综合考查了平行线和角平分线的性质，等腰三角形的性质及判定．
练习册系列答案
相关题目
如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
