题目内容
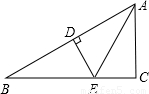
如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
解：DE垂直平分AB，
∴BE=AE=4．
故∠AEC=2∠B=60°．
sin60°=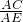
∵AC=2
．
分析：根据线段垂直平分线的性质得AE=BE=4；∠AEC=2∠B=60°．易求AC．
点评：本题考查的是线段垂直平分线的性质（垂直平分线上任意一点，和线段两端点的距离相等）有关知识．
∴BE=AE=4．
故∠AEC=2∠B=60°．
sin60°=
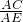
∵AC=2
．分析：根据线段垂直平分线的性质得AE=BE=4；∠AEC=2∠B=60°．易求AC．
点评：本题考查的是线段垂直平分线的性质（垂直平分线上任意一点，和线段两端点的距离相等）有关知识．
练习册系列答案
相关题目
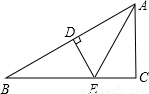
如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
