题目内容
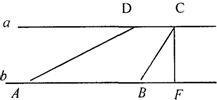 23、如图,河流两岸a,b互相平行,C,D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=32°,然后沿河岸走了100m到达B处,测得∠CBF=64°,求河流的宽度CF的值?(结果精确到0.1m).参考数据:
23、如图,河流两岸a,b互相平行,C,D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=32°,然后沿河岸走了100m到达B处,测得∠CBF=64°,求河流的宽度CF的值?(结果精确到0.1m).参考数据:| 角度α | sinα | cosα | tanα |
| 32° | 0.53 | 0.85 | 0.62 |
| 64° | 0.9 | 0.44 | 2.05 |
分析:根据四边形AECD是平行四边形得出BC=BE,再根据三角函数进而得出CF=CB•sin64°,即可得出CF的值.
解答:解:过C作CE∥AD,交AB于E.(如图)(1分)
∵CD∥AE,CE∥AD,
∴四边形AECD是平行四边形,(2分)
∴AE=DC=50,BE=100-50=50,∠CEB=∠DAB=32°,
又∠CBF=64°,
∴∠ECB=32°,
∴BC=BE=50,(4分)
∴在Rt△CFB中,CF=CB•sin64°=50×0.9≈45(米).(4分)
答:河流的宽度CF的值约为45米.(1分)
故河流的宽度CF的值为45m.
∵CD∥AE,CE∥AD,

∴四边形AECD是平行四边形,(2分)
∴AE=DC=50,BE=100-50=50,∠CEB=∠DAB=32°,
又∠CBF=64°,
∴∠ECB=32°,
∴BC=BE=50,(4分)
∴在Rt△CFB中,CF=CB•sin64°=50×0.9≈45(米).(4分)
答:河流的宽度CF的值约为45米.(1分)
故河流的宽度CF的值为45m.
点评:本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线产生直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
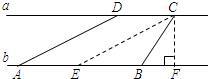 4、如图,河流两岸a,b互相平行,C,D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值.(结果精确到个位)
4、如图,河流两岸a,b互相平行,C,D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值.(结果精确到个位)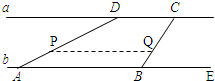 岸b上的A处测得∠DAB=30°,塑料瓶正好在AD上的P处,然后沿河岸用了20秒走了100m到达B处,测得∠CBE=60°,塑料瓶也漂流到了BC上的Q处.
岸b上的A处测得∠DAB=30°,塑料瓶正好在AD上的P处,然后沿河岸用了20秒走了100m到达B处,测得∠CBE=60°,塑料瓶也漂流到了BC上的Q处.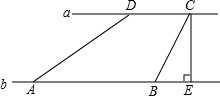 (2012•贵阳模拟)如图,河流两岸a、b互相平行,C,D是河岸a上间隔50m的两个电线杆,某人在河岸b上的A处测得∠DAB=35°,然后沿河岸走了100m到达B处,测得∠CBE=62°,作CE⊥b于点E,求河流的宽度CE(结果精确到个位).
(2012•贵阳模拟)如图,河流两岸a、b互相平行,C,D是河岸a上间隔50m的两个电线杆,某人在河岸b上的A处测得∠DAB=35°,然后沿河岸走了100m到达B处,测得∠CBE=62°,作CE⊥b于点E,求河流的宽度CE(结果精确到个位).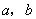 互相平行,C,D是河岸
互相平行,C,D是河岸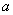 上间隔50m的两个电线杆,某人在河岸
上间隔50m的两个电线杆,某人在河岸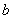 上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值(结果精确到个位).
上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值(结果精确到个位).