Question

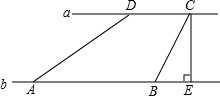（2012•贵阳模拟）如图，河流两岸a、b互相平行，C，D是河岸a上间隔50m的两个电线杆，某人在河岸b上的A处测得∠DAB=35°，然后沿河岸走了100m到达B处，测得∠CBE=62°，作CE⊥b于点E，求河流的宽度CE（结果精确到个位）．

Answer 1

分析：过点C作CE∥AD，交AB于E，再根据CD∥AE，CE∥AD得到四边形AECD是平行四边形．然后分别在Rt△CFE中和Rt△CBE中表示出EF和BE，利用两者的差为50求得CE的长即可；

解答：解：过点C作CF∥AD，交AB于F
∵CD∥AE，CF∥AD
∴四边形AFCD是平行四边形．
∴AF=CD=50m，∠DAB=∠CFE=35°，
在Rt△CFE中，

CE

EF

=tan35°，
∴EF=

CE

tan35°

，
在Rt△CBE中，

CE

BE

=tan62°，
∴BE=

CE

tan62°

，
∵BF=AB-AF=100-50=50，
∴EF-BE=

CE

tan35°

-

CE

tan62°

=50，
∴CE≈56，
答：河宽CE为56米．

点评：此题考查的是解直角三角形的应用-河流的宽度问题，提供了一个与现实生活密切联系的问题情境，以考查学生对有关知识的理解和运用所学知识的能力，关键是要作出辅助线利用条件由两个直角三角形列出关于河宽CE的方程求解．难度中等．