题目内容
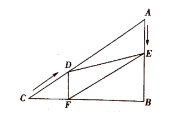
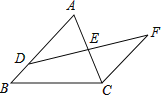
【题目】如图,在△ABC 中,∠BAC=90°,分别以 AC 和 BC 为边向外作正方形 ACFG 和正方形 BCDE,过点 D 做 FC 的延长线的垂线,垂足为点 H.
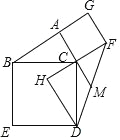
(1)求证:△ABC≌△HDC;
(2)连接 FD,交 AC 的延长线于点 M,若 AG=![]() ,tan∠ABC=
,tan∠ABC= ![]() ,求△FCM 的面积.
,求△FCM 的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先判断出∠ACB=∠HCD,即可得出结论;(2)先求出△ABC 的面积,进而求出 S△HDC=S△ABC=![]() ,进而得出 S△DHF=2S△CDH=
,进而得出 S△DHF=2S△CDH= ![]() ,再判断出△FCM∽△FHD,即可得出结论.
,再判断出△FCM∽△FHD,即可得出结论.
(1)∵四边形 BCDE 是正方形,
∴BC=CD,∠BCD=90°,
∵四边形 ACFG 是正方形,
∴CF=AG=AC,∠ACF=∠ACH=90°,
∴∠ACB=∠HCD,
∵DH⊥CF,
∴∠H=90°=∠BAC,
在△ABC 和△HDC 中, ,
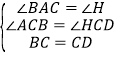 ,
,
∴△ABC≌△HDC;
(2)∵AG= ![]() ,
,
∴AC=![]() ,
,
在 Rt△ABC 中,tan∠ABC=![]() ,
,
∴AB= ![]() AC=
AC= ![]() ,
,
∴S△ABC= ![]() AB×AC=
AB×AC= ![]() ,
,
∵△ABC≌△HDC,
∴S△HDC=S△ABC=![]() ,AC=CH,
,AC=CH,
∴CH=CF,
∴S△DHF=2S△CDH=![]() ,
,
∵∠FCM=∠H=90°,
∴CM∥HD,
∴△FCM∽△FHD,
∴![]() ,
,
∴S△FCM= ![]() S△FHD=
S△FHD=![]() .
.

练习册系列答案
相关题目