题目内容
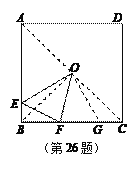
【题目】如图1,点O为正方形ABCD 的中心,E为AB 边上一点,F为BC边上一点,△EBF的周长等于 BC 的长.
(1)求∠EOF 的度数.
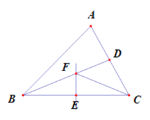
(2)连接 OA、OC(如图2).求证:△AOE∽△CFO.
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.

【答案】(1)45°;(2)证明见解析;(3)![]()
【解析】分析:(1)、在BC上取一点G,使得CG=BE,连接OB、OC、OG,然后证明△OBE和△OCG全等,从而得出∠BOE=∠COG,∠BEO=∠CGO,OE=OG,根据三角形的周长得出EF=GF,从而得出△FOE和△GOF全等,得出∠EOF的度数;(2)、连接OA,根据点O为正方形ABCD的中心得出∠OAE=∠FCO=45°,结合∠BOE=∠COG得出∠AEO=∠COF,从而得出三角形相似;(3)、根据相似得出线段比,根据相似比求出AE和CO的关系,CF和AO的关系,从而得出答案.
详解:解:(1)、如图,在BC上取一点G,使得CG=BE,连接OB、OC、OG.
∵点O为正方形ABCD的中心, ∴ OB=OC,∠BOC=90°,∠OBE=∠OCG=45°.
∴△OBE≌△OCG(SAS). ∴∠BOE=∠COG,∠BEO=∠CGO,OE=OG.
∴∠EOG=90°,∵△BEF的周长等于BC的长,
∴ EF=GF. ∴△EOF≌△GOF(SSS).∴∠EOF=∠GOF=45°.
(2)、连接OA.∵ 点O为正方形ABCD的中心, ∴∠OAE=∠FCO=45°.
∵∠BOE=∠COG, ∠AEO=∠BOE+∠OBE=∠BOE+45°,
∠COF=∠COG+∠GOF=∠COG+45°. ∴ ∠AEO=∠COF,且∠OAE=∠FCO.
∴ △AOE∽△CFO.
(3)、∵△AOE∽△CFO,∴![]() =
=![]() =
=![]() .即AE=
.即AE= ![]() ×CO,CF=AO÷
×CO,CF=AO÷![]() .
.
∵OE=![]() OF,∴
OF,∴![]() =
=![]() .∴AE=
.∴AE=![]() CO,CF=
CO,CF=![]() AO. ∴
AO. ∴![]() =
=![]() .
.