题目内容
求实数x、y的值,使得(y-1)2+(x+y-3)2+(2x+y-6)2达到最小值.
考点:函数最值问题
专题:
分析:首先假设a=y-1,b=x+y-3,c=2x+y-6,得出可得a-2b+c=-1,进而利用琴生不等式得出a2+b2+c2=a2+
b2+
b2+
b2+
b2+c2≥
(a-
b-
b-
b-
b+c)2,进而求出即可.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:a=y-1,b=x+y-3,c=2x+y-6,
可得a-2b+c=-1,
则原式=a2+b2+c2=a2+
b2+
b2+
b2+
b2+c2≥
(a-
b-
b-
b-
b+c)2=
(a-2b+c)2=
,
取等条件a=-
b=c,
即y-1=-
(x+y-3)=2x+y-6,
,
解得:
,
∴x=
,y=
,此时最小值
.
可得a-2b+c=-1,
则原式=a2+b2+c2=a2+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
取等条件a=-
| 1 |
| 2 |
即y-1=-
| 1 |
| 2 |
|
解得:
|
∴x=
| 5 |
| 2 |
| 5 |
| 6 |
| 1 |
| 6 |
点评:此题主要考查了函数最值问题,利用琴生不等式得出a2+b2+c2≥
(a-
b-
b-
b-
b+c)2是解题关键.
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
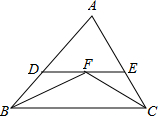 如图,△ABC中,DE∥BC,FB,FC分别平分∠B和∠C,已知BC=20,AB=18,AC=16,则△ADE的周长是( )
如图,△ABC中,DE∥BC,FB,FC分别平分∠B和∠C,已知BC=20,AB=18,AC=16,则△ADE的周长是( )| A、30 | B、32 | C、34 | D、36 |
 如图,在等腰三角形ABC中,AB=AC,D,E为AC边的三等分点,则BD+BE与3AB的大小关系是
如图,在等腰三角形ABC中,AB=AC,D,E为AC边的三等分点,则BD+BE与3AB的大小关系是