题目内容
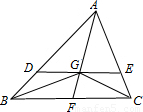
过△ABC的重心G作BC的平行线，分别交AB、AC于点D、E，则S△GBC：S△ADE=________．
3：4
分析：利用重心的性质得出AG：AF=DE：BC=2：3，以及△ADE与△GBC高的比值为2：1，底边比值为2：3，即可得出S△GBC：S△ADE的值．
解答：如图，过G作DE∥CG交AB于E，
∵过重心G作BC的平行线，
∴DE∥BC，
∴△ADE∽△ABC，
AG：AF=DE：BC=2：3，
∵△ADE与△GBC高的比值为2：1，底边比值为2：3，
∴S△GBC：S△ADE=3：4，
故答案为：3：4．
点评：此题考查了重心的知识和相似三角形的判定与性质以及平行线分线段成比例定理，得出三角形底与高的比值是解决问题的关键．
分析：利用重心的性质得出AG：AF=DE：BC=2：3，以及△ADE与△GBC高的比值为2：1，底边比值为2：3，即可得出S△GBC：S△ADE的值．
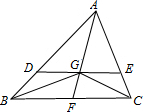
解答：如图，过G作DE∥CG交AB于E，
∵过重心G作BC的平行线，
∴DE∥BC，
∴△ADE∽△ABC，
AG：AF=DE：BC=2：3，
∵△ADE与△GBC高的比值为2：1，底边比值为2：3，
∴S△GBC：S△ADE=3：4，
故答案为：3：4．
点评：此题考查了重心的知识和相似三角形的判定与性质以及平行线分线段成比例定理，得出三角形底与高的比值是解决问题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
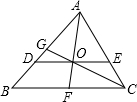如图，过△ABC的重心O点（三条中线的交点），作BC的平行线，交AB于D，交AC于E，则△ADE与△ABC的面积比是（ ）| A、1：2 | B、2：3 | C、1：3 | D、4：9 |
11、过△ABC的重心G作BC的平行线，分别交AB、AC于点D、E，则S△GBC：S△ADE=
如图，过△ABC的重心O点（三条中线的交点），作BC的平行线，交AB于D，交AC于E，则△ADE与△ABC的面积比是