题目内容
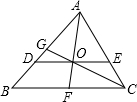 如图,过△ABC的重心O点(三条中线的交点),作BC的平行线,交AB于D,交AC于E,则△ADE与△ABC的面积比是( )
如图,过△ABC的重心O点(三条中线的交点),作BC的平行线,交AB于D,交AC于E,则△ADE与△ABC的面积比是( )| A、1:2 | B、2:3 | C、1:3 | D、4:9 |
分析:如图,过F作FH∥CG交AB于H,根据平行线分线段成比例定理,由F为BC中点,得到BH=HG=
BG=
AG,又因为OG∥FH,则AO:AF=AG:AH=AG:(AG+HG)=1:(1+
)=2:3,再根据DE∥BC,得到△ADE∽△ABC,AO:AF=AE:AC,然后根据相似三角形面积的比等于相似比的平方即可得到△ADE与△ABC的面积比.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: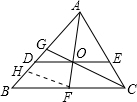 解:如图,过F作FH∥CG交AB于H,
解:如图,过F作FH∥CG交AB于H,
∵F为BC中点,
∴BH=HG=
BG=
AG,
∵OG∥FH,
∴AO:AF=AG:AH=AG:(AG+HG)=1:(1+
)=2:3,
又∵DE∥BC,
∴△ADE∽△ABC,AO:AF=AE:AC,
∴S△ADE:S△ABC=AE2:AC2=AO2:AF2=4:9.
故选D.
 解:如图,过F作FH∥CG交AB于H,
解:如图,过F作FH∥CG交AB于H,∵F为BC中点,
∴BH=HG=
| 1 |
| 2 |
| 1 |
| 2 |
∵OG∥FH,
∴AO:AF=AG:AH=AG:(AG+HG)=1:(1+
| 1 |
| 2 |
又∵DE∥BC,
∴△ADE∽△ABC,AO:AF=AE:AC,
∴S△ADE:S△ABC=AE2:AC2=AO2:AF2=4:9.
故选D.
点评:本题考查了相似三角形的判定与性质以及平行线分线段成比例定理.也考查了相似三角形面积的比等于相似比的平方.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
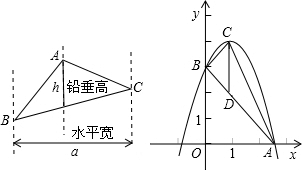

 阅读材料:
阅读材料: 如图,过△ABC的重心O点(三条中线的交点),作BC的平行线,交AB于D,交AC于E,则△ADE与△ABC的面积比是
如图,过△ABC的重心O点(三条中线的交点),作BC的平行线,交AB于D,交AC于E,则△ADE与△ABC的面积比是